【2023年CSP-J-初赛试卷及解析】
【单项选择题(1-15)】
参考:https://www.cnblogs.com/hellohebin/p/17709333.html
参考:https://mp.weixin.qq.com/s/oQwrXWkD3qXuiz92wet1wQ
参考:https://blog.csdn.net/guolianggsta/article/details/132940178
1、在C++中,下面哪个关键字用于声明一个变量,其值不能被修改?( )
A.unsigned
B.const
C.static
D.mutable
【答案】:B
【解析】
unsigned 表示无符号型变量,即不能存储负数。
unsigned int a = 0xffffffff; cout << a; // 4294967295
4294967295 表示 32位 无符号整数的十进制最大值。
如果是16进制,那么是 0xFFFFFFFF 。也可以解释为一个IP地址(V4) 255.255.255.255
当无符号时,最大的数为 4294967295 ;当有符号时,第一位是符号位,所以最大的正数为 2147483647 。
const 是常态变量(constant不变的 的缩写),表示该变量的值不能被修改。
由 const 修饰的成员函数中,不能对成员变量进行修改,因为隐藏的形参是 const 属性的。
static 静态变量,表示该变量的作用域仅限于当前文件或当前函数内,不会被其他文件或函数访问。
void f(){
static int a = 0;
a++;
cout << a << endl;
}
int main() {
f(); // 1
f(); // 2
return 0;
}
mutable 使变量在类的非成员函数中也可以被修改。
2、八进制数12345670(8)和07654321(8)的和为( )
A.22222221(8)
B.21111111(8)
C.22111111(8)
D.22222211(8)
【答案】:D
【解析】
参考十进制的逢十进一的计算方法,八进制就是逢八进一。
12345670(8) +07654321(8) =22222211(8)
3、阅读下述代码, 请问修改data的value成员以存储3.14, 正确的方式是( )
union Data{
int num;
float value;
char symbol;
};
union Data data;
A.data.value = 3.14;
B.value.data = 3.14;
C.data->value = 3.14;
D.value->data = 3.14;
【答案】:A
【解析】
本段代码是一个 union (中译:联合体、共用体),联合体的浮点数成员直接用“.”进行访问。“->”用于指针的访问。
union和struct都是由不同的数据类型成员组成的,结构体所有成员占用的内存空间是累加的,而联合体中所有的成员共用一块地址空间。可以参考struct,访问其成员变量使用【类型变量名.成员变量名】,即【data.value】。
联合体的所有成员占用同一段内存,修改一个成员会影响其余所有成员。联合体占用的内存等于最长的成员占用的内存。
联合体使用了内存覆盖技术,同一时刻只能保存一个成员的值,如果对新的成员赋值,就会把原来成员的值覆盖掉。
如该 union 中最大内存为 float value,占用 4Byte,该 Data 也占用 4Byte。
4、假设有一个链表的节点定义如下:
struct Node {
int data;
Node* next;
}
现在有一个指向链表头部的指针:Node* head, 如果想要在链表中插入一个新节点,其成员data的值为42, 并使新节点成为链表的第一个节点, 下面哪个操作是正确的?
A.Node* newNode = new Node; newNode->data=42; newNode->next = head; head = newNode;
B.Node* newNode = new Node; head->data=42; newNode->next = head; head = newNode;
C.Node* newNode = new Node; newNode->data=42; head->next = newNode;
D.Node* newNode = new Node; newNode->data=42; newNode->next = head;
【答案】:A
【解析】
第一句,4个选项均相同,表示定义Node类型newNode。
第二句表示将其成员的data的值设为42,使用newNode->data = 42。因为newNode要成为第一个节点,所以newNode->next需要指向现有的head,即newNode->next = head。此时newNode变为了head,所以A与D相比多了个这一句,head = newNode。
5、根节点的高度为1,一棵拥有2023个节点的三叉树高度至少为( )
A.6
B.7
C.8
D.9
【答案】:C
【解析】
三叉树:节点度最大为3的树。
假设这是一棵高度为 \(k\) 的满三叉树,那么其节点数为 \(\sum\limits_{i=0}^k{3^i}\ge{2023}\) ,解得 \(k\ge8\) 。
推导法:“至少为”说明要求高度最小的值,画完全三叉树可以满足题目要求。第1层1个节点,第2层3个节点,第3层9个节点,第4层27个节点,第5层81个节点,第6层243个节点,第7层729个节点,第8层2187个节点。前7层相加为1093,不足2023,加上第8层超过2023,所以至少8层。
6、小明在某一天中依次有七个空闲时间段,他想要选出至少一个空闲时间段来练习唱歌,但他希望任意两个练习的时间段之间都有至少两个空闲的时间段让他休息。则小明一共有( )种选择时间段的方案。
A.31
B.18
C.21
D.33
【答案】:B
【解析】
假设七个时间段为1234567,依次枚举n个时间段的组合数。
选择1个时间段,有7种 1、2、3、4、5、6、7
选择2个时间段,有4+3+2+1=10种:14、15、16、17、25、26、27、36、37、47
选择3个时间段,有1种:147
所以一共18种,选B。
7、以下关于高精度运算的说法错误的是( )
A.高精度计算主要是用来处理大整数或需要保留多位小数的运算。
B.大整数除以小整数的处理的步骤可以是,将被除数和除数对齐,从左到右逐位尝试将除数乘以某个数,通过减法得到新的被除数,并累加商。
C.高精度乘法的运算时间只与参与运算的两个整数中长度较长者的位数有关。
D.高精度加法运算的关键在于逐位相加并处理进位。
【答案】:C
【解析】
高精度乘法的时间复杂度为参与运算的两个整数的长度的位数的乘积。
选 C 。
具体高精度计算实现可以参考洛谷P1303题解。
网址:https://www.luogu.com.cn/article/pxfpoeoi
8、后缀表达式“623+-382/+*2^3+”对应的中级表达式是( )。
A.((6-(2+3))*(3+8/2))^2+3
B.6-2+3*3+8/2^2+3
C.(6-(2+3))*((3+8/2)^2)+3
D.6-((2+3)*(3+8/2))^2+3
【答案】:A
【解析】
要点:将一个表达式看作一个数,用ab+的形式进行替换,主要是手动练习。
前缀表达式:+ab
中缀表达式:a+b
后缀表达式:ab+
中缀变后缀有3个步骤,第一步加括号,第二步将运算符移到括号右边,第三步去除括号。这里反着做一遍。
加括号:((((6(23)+)-(3(82)/)+)*2)^3)+
括号移到中间:((((6-(2+3))*(3+(8/2)))^2)+3)
逐步移除多余括号,得到:((6-(2+3))*(3+8/2))^2+3
选 A 。
9、数101010(2)和166(8)的和为( )。
A.10110000(2)
B.236(8)
C.158(10)
D.A0(16)
【答案】:D
【解析】
统一换算成十进制数后计算。
101010(2)=42(10)
166(8)=118(10)
160(10)=A0(16)=240(8)=10100000(2)
选 D 。
快速计算:
8进制使用一分三转换为 2进制。
166(8)=001110110(2)
101010(2) +1110110(2) = 10100000(2) = 240(8) = A0(16) = 0XA0 =0xa0
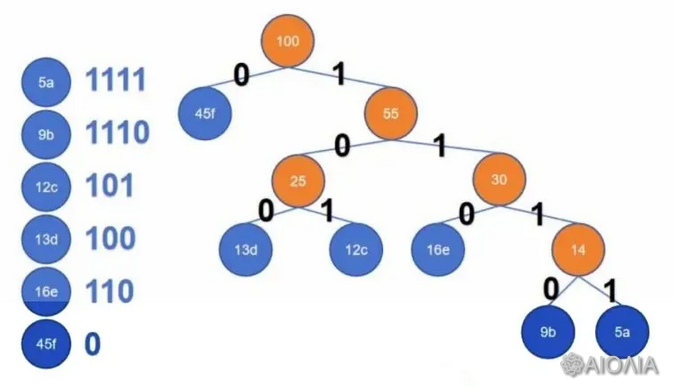
10、假设有一组字符{a,b,c,d,e,f},对应的频率分别为5%、9%、12%、13%、16%、45%。请问以下哪个选项是字符a,b,c,d,e,f分别对应的一组哈夫曼编码?( )
A.1111,1110,101,100,110,0
B.1010,1001,1000,011,010,00
C.000,001,010,011,10,11
D.1010,1011,110,111,00,01
【答案】:A
【解析】
哈夫曼编码:每次选最小的两个元素组合成一个新元素,由此构建一棵二叉树,为左边赋值0,右边赋值1,到一个节点经过的边的值按顺序构成的就是哈夫曼编码,其编码的数值不固定,但长度固定。
按照哈夫曼规则画出哈夫曼树,f节点没有子节点,观察答案A,说明f为0,通过排除法可以直接选A。
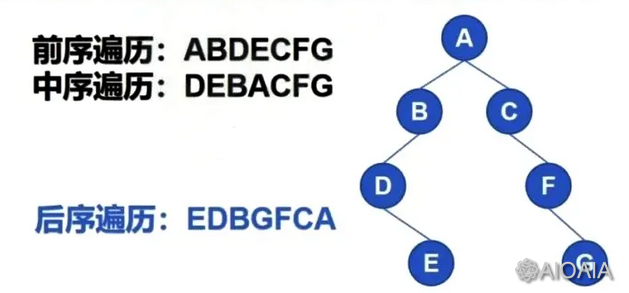
11、给定一棵二叉树, 其前序遍历结果为:ABDECFG, 中序遍历结果为:DEBACFG。请问这棵树的正确后序遍历结果是什么?( )
A.EDBGFCA
B.EDGBFCA
C.DEBGFCA
D.DBEGFCA
【答案】:A
【解析】
中序遍历是先访问左子树,然后访问根,再访问右子树。
前序遍历是先访问根,然后访问左子树,再访问右子树。
后续遍历是先访问左子树,然后访问右子树,再访问根。
根据前序和中序遍历,可以画出二叉树,后序遍历为EDBGFCA,选A
12、考虑一个有向无环图,该图包含4条有向边:(1,2),(1,3),(2,4)和(3,4)。以下哪个选项是这个有向无环图的一个有效的拓扑排序?( )
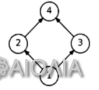
A.4,2,3,1
B.1,2,3,4
C.1,2,4,3
D.2,1,3,4
【答案】:B
【解析】
访问2、3前需要先访问1,访问4前需要先访问2或3,选 B 。
拓扑排序:选择当前入度为0的点,并删除与之相连的边,重复此过程,直到所有点都选过。选点的顺序就是一个拓扑序,其不唯一。
13、在计算机中,以下哪个选项描述的数据存储容量最小?( )
A.字节(byte)
B.比特(bit)
C.字(word)
D.千字节(kilobyte)
【答案】:B
【解析】
存储容量的最小的单位是位(bit)。
处理数据最基本的单位是字节(byte)。
14、一个餐有10个男生和12个女生,如果要选出一个3人的小组,并且小组中必须至少包含1个女生,那么有多少种可能的组合?( )
A.1420
B.1770
C.1540
D.2200
【答案】A
【解析】
选1个女生,组合=C(12,1)*C(10,2)=540
选2个女生,组合=C(12,2)*C(10,1)=660
选3个女生,组合=C(12,3)=220
共计1420种组合
15、以下哪个不是操作系统?( )
A.Linux
B.Windows
C.Android
D.HTML
【答案】D
【解析】
HTML是超文本标记语言,不是操作系统。
【阅读程序题(16-32)】
二、阅读程序(程序输入不超过数组成字符串定义的范围:判断题正确填√,错误填×;除特殊说明外,判断题1.5分,选择题3分,共计40分)
(1)
01 #include<iostream>
02 #include<cmath>
03 using namespace std;
04
05 double f(double a,double b,double c){
06 double s=(a+b+c)/2;
07 return sqrt(s*(s-a)*(s-b)*(s-c));
08 }
09
10 int main(){
11 cout.flags(ios::fixed);
12 cout.precision(4);
13
14 int a,b,c;
15 cin>>a>>b>>c;
16 cout<<f(a,b,c)<<endl;
17 return 0;
18
}
假设输入的所有数都为不超过 1000 的正整数,完成下面的判断题和单选题:
【程序解析】
给定三角形的3条边长,使用海伦公式求面积,结果保留 4 位小数。
本程序较为简洁,最重要的部分是函数f。阅读 f 的返回值计算方式可知,这是计算三角形面积的海伦公式,其将 a、b、c 作为浮点数处理,考虑到了三角形面积可能非整数的情形。
值得注意:主函数中用到了平时学习较为少见的 cout 处理方式,其中:
cout.flags(ios::fixed) 表示以定点形式显示浮点数。如果没有这一句,则输出会形如 1e4 这样的科学计数法,
cout.precision(4) 则是指定小数位数为 4 位。
这里有一个坑:常用的 setprecision 方法,在输出浮点数时,不会保留尾随 0 ,而本程序中以上两句的结合,会对 0.1 这样的浮点数,输出 0.1000 ,其携带尾随 0 。
判断题
16.(2分)当输入为“2 2 2”时,输出为“1.7321”( )
【答案】True
【解析】等边三角形面积求解,或者直接带入程序,得到 \(\sqrt{3}\) 。
如果能够记得常用根式的小数点后4位展开,则可以快速判断。
然而常常只记得 1.732 ,即小数点后3位,则需依次反向计算 1.7320、1.7321和1.7322 的平方,观察哪一项最接近 3。
考场上怎样计算平方根到小数点后4位?
参考:https://aiolia.org/sqrt
17. (2分)将第7行中的”(s-b)*(s-c)”改为”(s-c)*(s-b)”不会影响程序运行的结果( )
【答案】True
【解析】乘法满足交换律,且从程序的角度来考虑, double 类型的 s , a , b , c 的计算在输入不超过 1000 时,不会发生溢出。所以 sqrt 开根号的值不变,不影响程序的运行结果,
此类问题需要注意的是交换后是否会影响数据范围,精度,计算原理。
18.(2分)程序总是输出四位小数( )
【答案】True
【解析】main 函数开始的位置已设置输出格式,如果没有取消该格式,会一直持续。当a、b、c无法构成面积时,计算结果为0.0000,也仍然保留四位小数。
单选题
19. (3分)当输入为“3 4 5”时,输出为( )
A. “6.0000”
B. “12.0000”
C. “24.0000”
D. “30.0000”
【答案】A
【解析】直角三角形面积求解,或者带入计算。
边长为 3 , 4 , 5 是典型的直角三角形,面积为 6 。在本程序中还需要在小数点后补上 4 个 0 。
20.(3分)当输入为“5 12 13”时,输出为( )
A. “24.0000”
B. “30.0000”
C. “60.0000”
D. “120.0000”
【答案】B
【解析】直角三角形面积求解,或者带入计算。
(2)
01 #include<iostream>
02 #include<vector>
03 #include<algorithm>
04 using namespace std;
05
06 int f(string x,string y){
07 int m=x.size();
08 int n=y.size();
09 vector<vector<int>>v(m+1,vector<int>(n+1,0));
10 for(int i=1;i<=m;i++){
11 for(int j=1;j<=n;j++){
12 if(x[i-1]==y[j-1]){
13 v[i][j]=v[i-1][j-1]+1;
14 }else{
15 v[i][j]=max(v[i-1][j],v[i][j-1]);
16 }
17 }
18 }
19 return v[m][n];
20 }
21
22 bool g(string x,string y){
23 if(x.size() != y.size()){
24 return false();
25 }
26 return f(x+x,y)==y.size();
27 }
28
29 int main(){
30 string x,y;
31 cin>>x>>y;
32 cout<<g(x,y)<<endl;
33 return 0;
34 }
程序意义:给定两个字符串,如果字符串x,y长度相等,将x变为 xx,求xx 与 y的最长子序列长度。
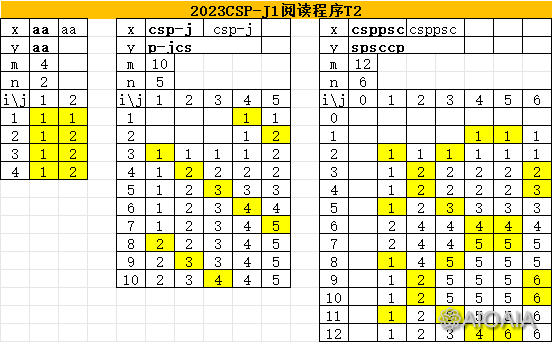
程序以 f 和 g 两个函数为主,其中对 STL 的考察与去年类似– f 函数中使用到了 vector 套 vector 的用法,部分同学可能学习过 vector 容器的用法,但二维 vector 可能一时无法理解。然而,对 STL 的“冷门”考察,一定能够从程序的上下文中找到答案。只要观察接下来 v 的用法,就会发现,可以把它当做是一个二维数组。
f 函数实际考察动态规划中的最长公共子序列(LCS),作为一个经典知识点,这里省去推导,直接给出结论:v[i][j] 表示字符串 x 的第 1 ~ i 位和字符串 y 的第 1 ~ j 位的最长公共子序列的长度。
对于一个字符串,其子序列指的是可以在字符串中任意删掉一些字符后剩下的部分,比如 bd 是 abcd的子序列,c 和 a 也是 abcd 的子序列,公共子序列则要求同时是两个字符串的子序列。
最后,g 函数先筛去两个字符串长度不一致的情况,然后对于字符串 x,在其末尾再复制一份,这一变换形如 abcd》abcdabcd,判断变换后的双倍 x 和 y 的最长公共子序列长度是否等于 y 的原长度。
判断题
21.(1.5分)f函数的返回值小于等于min(n,m)。( )
【答案】True
【解析1】f 函数返回两个字符串的最长公共子序列长度,最好情况下,这一公共子序列也只能恰好等于其中某一字符串,其长度不能再超过字符串 x 和 y 的长度,而 m 和 n 分别代表 x 和 y 的长度,故正确。
【解析2】返回两个字符串的最长公共子序列长度,肯定不会超过某一个字符串的长度
22. (1.5分)f函数的返回值等于两个输入字符串的最长公共子串的长度。( )
【答案】False
【解析1】
子串一定连续,子序列不一定连续,二者中元素的相对位置无改变。
子串与子序列是两个不同的概念,其中子串要求字符必须在原字符串中连续出现,而子序列则只对顺序有要求。例如:ace 是 abcde 的子列,但不是其子串;cab 既是 abcabc 的子串,又是其子序列。实际上,一个字符串的子串,一定是原串的子序列,但反之不然。
【解析2】子串不等于子序列,子串要求字符在原字符串中连续出现,而子序列只有顺序要求
23. (1.5分)当输入两个完全相同的字符串时,g函数的返回值总是true( )
【答案】True
【解析1】输入的 x 和 y 相同时,x + x 等于 y + y ,其和 y 的最长公共子串恰为 y 本身,故 g 选项返回的判断条件成立。
【解析2】两个相同的字符串,公共子序列长度等于y字符串的长度,所以正确。
单选题
24.(3分)将第19行中的“v[m][n]”替换为“v[n][m]”,那么该程序( )
A. 行为不变
B. 只会改变输出
C. 一定非正常退出
D. 可能非正常退出
【答案】D
【解析1】STL 容器有非常严格的使用要求,以一维情形举例,如果定义了
vectora(100,0)
,表示 a 的下标范围是 0~99 ,此时如果下标访问了 a[100] ,则一定会使程序非正常退出,二维的情形类似。如果替换为 v[n][m] ,在 n = m ,也就是两个字符串长度一致时,程序行为不变但如果 n ≠ m ,则会导致某一维的下标访问越界,此时一定非正常退出。综合而言,互换会导致可能非正常退出。
【解析2】:换为v[n][m],可能某一维下标访问会越界,此时会非正常退出。
25. 当输入为 “csp-j p-jcs” 时,输出为( )
A. “0”
B. “1”
C. “T”
D. “F”
【答案】B
【解析1】
布尔类型的输出,它会以 0 1 形式进行输出,而不是输出TRUE,FALSE,T,F等。
此时将求 csp-jesp-j和 p-jcs 的最长公共子序列,可知后者恰为前者的子串,故 g 函数返回的判断条件成立。注意输出的恰为 g 函数返回的 bool 值,需要排除 T 和 F。
【解析2】如果一看代码就知道是求最长公共子序列,那直接可以得到答案。如果不了解,可以尝试打表,二维列表中的元素值为v[i][j]。具体打完的表如下:
i 0 1 2 3 4 5 j 0 0 0 0 0 0 0 1 0 0 0 0 1 1 2 0 0 0 0 1 2 3 0 1 1 1 1 2 4 0 1 2 2 2 2 5 0 1 2 3 3 3 6 0 1 2 3 4 4 7 0 1 2 3 4 5 8 0 1 2 3 4 5 9 0 1 2 3 4 5 10 0 1 2 3 4 5
v[5][5]等于5,与y字符串长度相同,选 B 。
26. 当输入为“csppsc spsccp”时,输出为:( )
A. “T”
B. “F”
C. “0”
D. “1”
【答案】D
【解析1】此时将求 csppsccsppsc 和 spsccp 的最长公共子序列,从前者依次选出第 2、3、5、6、7、9 个字符,恰为 spsccp ,可知后者是前者的子序列,故 g 函数返回的判断条件成立。
【解析2】同25题,如果一下子看出是求最长公共子序列,那直接可以得到答案。如果不了解,可以尝试打表,二维列表中的元素值为v[i][j]。具体打完的表如下:
i 0 1 2 3 4 5 6 j 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 2 0 1 1 1 1 1 1 3 0 1 2 2 2 2 2 4 0 1 2 2 2 2 3 5 0 1 2 3 3 3 3 6 0 1 2 3 4 4 4 7 0 1 2 3 4 5 5 8 0 1 2 3 4 5 5 9 0 1 2 3 4 5 6 10 0 1 2 3 4 5 6 11 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6
v[14][6]等于6,与y字符串长度相同,选D。
(3)
01 #include <iostream>
02 #include <cmath>
03 using namespace std;
04
05 int solve1(int n){
06 return n*n;
07 }
08
09 int solve2(int n){
10 int sum=0;
11 for(int i=1;i<=sqrt(n);i++){
12 if(n%i==0){
13 if(n/i==i){
14 sum+=i*i;
15 }else{
16 sum+=i*i+(n/i)*(n/i);
17 }
18 }
19 }
20 return sum;
21 }
22
23 int main(){
24 int n;
25 cin>>n;
26 cout<<solve2(solve1(n))<<" "<<solve1((solve2(n)))<<endl;
27 return 0;
28 }
程序意义:solve1(n) 求n的平方,solve2(n) 求 n 的因子平方和。
本题考察约数。函数 solvel 返回参数 n 的平方;函数 solve2 返回参数 n 的约数的平方和。主函数对两个函数复合调用,先输出 n 的平方的约数平方和,再输出 n 的约数平方和的平方。
假设输入的n是绝对值不超过1000的整数,完成下面的判断题和单选题。
判断题
27.(2分)如果输入的 n 为正整数,solve2 函数的作用是计算 n 所有的因子的平方和( )
【答案】True
【解析1】solve2 的作用是返回 n 的所有约数的平方和。
【解析2】通过第32题带入计算,n=5时,solve(25)得到651,可以推算出solve2函数的作用就是计算n的所有因子的平方和,即1+25+625=651
28.(2分)第13~14行的作用是避免n的平方根因子i(或n/i)进入第16行而被计算两次( )
【答案】True
【解析1】枚举约数时,如果 i 等于 n/i,这两个表达式就代表同一个约数(即 n 的平方根),所以需要第 13 行的判断避免它被重复计算。
【解析2】通过第32题带入计算,i=1时,第13-14行没有将其加到sum中,是在第16行被计算,所以描述正确。
29.(2分)如果输入的n为质数,solve2(n)的返回值为( )
【答案】True
【解析1】质数的约数只有1和本身。它们的平方和即为 \(n^2+1\)
【解析2】通过第32题带入计算,n=5时,solve2(5)为26,符合题目描述。
单选题
30.(4分)如果输入的n为质数p的平方,那么solve2(n)的返回值为( )
A. \(p^2+p+1\)
B. \(n^2+n+1\)
C. \(n^2+1\)
D. \(p^4+2p^2+1\)
【答案】B
【解析1】solve2 中求解的是 n 的因子的平方和,如果 n 为质数 p 的平方:
\(n=p^2\) 时,它的约数有 1、p、\(p^2\),它们的平方和等于 \(1+p^2+p^4\) 。
代入 \(n=p^2\) 可化为 \(n^2+n+1\)
【解析2】通过第32题,n=25,此时p=5,因为solve(25)=651,将p=5带入4个选项中,应该是p^4+p^2+1,D错误。将n=25带入4个选项中,B正确。
31.(3分)当输入为正整数时,第一项减去第二项的差值一定( )
A. 大于0
B. 大于等于0且不一定大于0
C. 小于0
D. 小于等于0且不一定小于0
【答案】D
【解析1】举例排除最为方便,当n=1和9时,…。也可以直接带关系推导。
【解析2】通过第32题,第一项减去第二项的差值为负数,所以A、B肯定错误。满足差值为0的数,就是这个数的平方等于这个数的各个因子的平方和。1就是这个数,所以选D。
32.(3分)当输入为“5”时,输出为( )
A. “651 625”
B. “650 729”
C. “651 676”
D. “652 625”
【答案】C
【解析1】直接将 5 带入计算
n=5,第一项=1+25+625=651;第二项=(1+25)^2=676。
【解析2】将5带入计算,solve2(solve(1))等于651,solve1(solve2(5))等于676,选C。
【完善程序题(33-42)】
三、完善程序(单选题,每小题3分,共计 3 分)
(1)(寻找被移除的元素)问题:原有长度为 n+1公差为1等升数列,将数列输到程序的数组时移除了一个元素,导致长度为 n 的开序数组可能不再连续,除非被移除的是第一个或最后之个元素。需要在数组不连续时,找出被移除的元素。试补全程序。
#include <iostream>
#include <vector>
using namespace std;
int find_missing(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == mid + ①) {
②;
} else {
③;
}
}
return ④;
}
int main() {
int n;
cin >> n;
vector<int> nums(n);
for (int i = 0; i < n; i++) cin >> nums[i];
int missing_number = find_missing(nums);
if (missing_number == ⑤) {
cout << "Sequence is consecutive" << endl;
} else {
cout << "Missing number is " << missing_number << endl;
}
return 0;
}
【程序解析】本题考察二分法。
在本程序中 find_missing 函数就是利用二分法来找到一个长度为 n 的数组中不连续的位置,从而找出被移除元素的值。只需通过二分找到从左往右第一处使得 nums[i] 不为 nums[0]+i 的的位置,那么在数组中被移除的数就是 nums[0]+i。
33. ①处应填( B)(3分)
A. 1
B. nums[0]
C. right
D. left
【答案】B
【解析1】若数组连续,一定有 nums[i]==nums[0]+i ,所以只需通过二分找到第一处使得 nums[i] 不为 nums[0]+i 的位置即可。因此二分的判断条件是nums[mid]==nums[0]+mid。因此选B。
【解析2】第9行可以判断出代码为二分搜索,所以第11行和第13行肯定是left和right两个指针的移动,故第10行应该是判断满足什么条件时,left指针需要移动。mid左侧为连续的数字时,left需要移动。num[mid]= mid+num[0]时,左侧数字是连续的,选B。
可以代入nums = [1,2,3,5,6]进行验算,第一次while循环,mid = 2,nums[2] == 3,满足nums[mid] == mid + num[0](3 == 2 + 1)。
34. ②处应填(A )(3分)
A. left=mid+1
B. right=mid-1
C. right=mid
D. left=mid
【答案】A
【解析1】若满足 33 题所填的判断条件,则说明此时的 mid 猜小了,实际不连续位置(第一处使得 nums[i] 不等于 nums[0]+i 的位置)一定在 mid 之后,所以需要更新二分的左端点,并更新为 mid+1 ,因此选择 A。
【解析2】mid 左侧数据满足连续时,left 指针需要移到 mid 的右侧,所以 A选项 left = mid+1 满足。
35. ③处应填(C )(3分)
A.left=mid+1
B.right=mid-1
C.right=mid
D.left=mid
【答案】C
【解析1】若不满 33 所填的判断条件,就说明 mid 有可能猜大了,实际不连续位置(第一处使得 nums[i] 不等于 nums[0]+i 的位置)一定不在 mid 之后,可以等于 mid 。所以需要更新二分的右端点,并更新为 mid ,因此选择 C。
【解析2】mid左侧数据不连续,则右侧数据肯定连续。因此需要把right指针改为mid,下一轮从mid的左侧区域开始查找。所以选 C。
36. ④处应填(A )(3分)
A.left+nums[0]
B.right+nums[0]
C.mid+nums[0]
D.right+1
【答案】A
【解析1】左端点 left 才能表示最终二分找到的答案(也即不连续位置),因此最终被移除的数就是 left+nums[0]。首先很容易排除 D,然后因为 mid 只出现在二分的过程中,而且 mid 的定义也在 while 里,也很容易排除 C。可能的问题:这里为何选择 A 而不选择 B,事实上二分模板中的书写习惯是 return left 。在一些情况下 return right 会出现问题,但在本题中实际上最后一定是 left==right,所以理论上填 B 也可以。
【解析2】当退出while循环时,一定是left指针指向那个被移除的数前面一个数,用left+nums[0]就可以得到被移除的数,所以选A。
37. ⑤处应填( D)(3分)
A.nums[0]+n
B.nums[0]+n-1
C.nums[0]+n+1
D.nums[n-1]
【答案】D
【解析1】当 n 个数字连续时,最终我们会得到,left=n-1,right=n-1。由 36 所填代码,我们返回的数字就是 nums[0]+n-1 与不连续位置出现在第 n 个数字返回的数值相同。因此我们需要对这两种情况进行讨论,如果 n 个数字连续,会满足 nums[n-1]==nums[0]+n-1 ,如果是刚好不连续位置在第 n 个数的话不会使得这个式子成立。因此如果返回数字等于 nums[n-1] 的话,就说明原来 n 个数连续。故而选择 D。
【解析2】题目描述中提到“除非被移除的是第一个或最后一个元素”,所以要打印“Sequence is consecutive”,只可能移除第一个或最后一个元素,4个选项D为最后一个元素,所以选 D 。
(2) (编辑距离)给定两个字符串,每次操作可以选择删除(Delete)、插入(Insert)、替换(Replace),一个字符,求将第一个字符串转换为第二个字符串所需要的最少操作次数。
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int min(int x,int y,int z){
return min(min(x,y),z);
}
int edit_dist_dp(string str1,string str2){
int m=str1.length();
int n=str2.length();
vector<vector<int>> dp(m+1,vector<int>(n+1));
for(int i=0;i<=m;i++){
for(int j=0;j<=n;j++){
if(i==0)
dp[i][j]=(1);
else if(j==0)
dp[i][j]=(2);
else if((3))
dp[i][j]=(4);
else
dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],(5));
}
}
return dp[m][n];
int main(){
string str1,str2;
cin>>str1>>str2;
cout<<"Mininum number of operation:"<<edit_dist_dp(str1,str2)<<endl;
return 0;
}
【程序解析】
先阅读 main 函数,可以得知代码读入了两个字符串之后输出了 edit_dist_dp 的返回值,因此重点关注 edit_dist_dp 函数;
11-13 行定义了 n 为 str1 的长度, m 为 str2 的长度,一个二维的 vector (可以当成二维数组) dp[0..m][0..n];
15-26 行是 dp 过程;
27 行为返回 dp[n][m],看完这一行就应该明白 dp 数组的含义,之后通过 dp状态将 15-26 行的空填出来;
dp[n][m] 表示将 str1 长度为 n 的前缀变成 str2 长度为 m 的前缀所需要的最少步数,特别注意 strl,str2 是 string,下标范围分别是 [0..m-1] 与 [0..n-1] 。
38. ①处应填( A)(3分)
A. j
B. i
C. m
D. n
【答案】A
【解析1】考察 dp[0][j] 的值,根据阅读得到的 dp 数组的含义,dp[0][j] 表示 strl 长度为 0 的前缀(空字符串)变成 str2 长度为 j 的前缀的最少步数,这里明显最少在空串内添加 str2 的前 j个字符,因此填 j 选 A 选项。
【解析2】
dp[m][n]表示长度为m的字符串变成长度为n的字符串最少步数,那么dp[0][j]就应该表示str1长度为0的字符串变成长度为j的字符串最少步数。显然应该是添加j个字符,所以选A
39. ②处应填(B )(3分)
A. j
B. i
C. m
D. n
【答案】B
【解析1】考察 dp[i][0] 的值,根据阅读得到的 dp 数组的含义,dp[i][0] 表示 str1 长度为 i 的前缀变成 str2 长度为 0 的前缀(空字符串)的最少步数,这里明显最少是将 strl 的前 i 个字符全部删除,因此填 i 选 B 选项。
【解析3】dp[m][n] 表示长度为m的字符串变成长度为n的字符串最少步数,那么 dp[i][0] 就应该表示 str1 长度为 i 的字符串变成长度为 0 的字符串最少步数。显然应该是删除 i 个字符,所以选 B。
40. ③处应填(A )(3分)
A. str1[i-1]==str2[j-1]
B. str1[i]==str2[j]
C. str1[i-1]!=str2[j-1]
D. str1[i]!=str2[j]
【答案】A
【解析1】考察编辑距离 dp 转移,需要阅读 22-24 行的代码可知这里应该是两个字符相等不需要操作的情况,也就是 strl 的第 i 个字符与 str2 的第 j 个字符相等的情况,但是要特别注意的是这一问埋了大坑,strl 的第 i 个字符是 strl[i-1],不要跳进去了,选 A。
【解析2】因为第24行应该是判断str1和str2某个位置字符不相等时的处理,故这里就应该是字符相等的位置。str1和str2的第i个字符应该是str1[i-1],选A
41. ④处应填(B )(3分)
A. dp[i-1][j-1]+1
B. dp[i-1][j-1]
C. dp[i-1][j]
D. dp[i][j-1]
【答案】B
【解析1】40 题时已经说过,如果两个字符相等的话,不需要操作,因此将 str1前 i 个字符变成 str2 前 j 个字符需要的最少步数就与将 strl 前 i-1 个字符变成 str2 前 j-1 个字符是一样的,填 dp[i-1][j-1],选 B。
【解析2】这里是动态规划的基本概念,如果两个字符相等,str1 的i字符变成str2 的 j 个字符最少步数,就等于 str 的 i-1 个字符变成 str2 的 j-1 个字符的最少步数。选 B 。
42. ⑤处应填( C)(3分)
A. dp[i][j] + 1
B. dp[i-1][j-1]+1
C. dp[i-1][j-1]
D. dp[i][j]
【答案】C
【解析1】
这里有一个在上面定义的 min 函数,功能是对三个整数求最小值,观察第 24 行 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],?) 由前面的 1+ 可知这里进行了一次操作,那么 dp[i][j-1] 就对应着插入,dp[i-1][j] 对应着删除,剩下要填的就是替换了,填 dp[i-1][j-1],选 C。
【解析2】
3个数字应该分别对应着插入、删除和替换。插入的话,就是相当于i比j多1,dp[i][j-1]就对应着插入。删除的话,就是相当于i比j少1,dp[i-1][j]就对应着删除。替换的话,i和j的数量相等,C选项满足要求。
5个空选出来后,可以带入abc和abd字符进行验算。打表如下:
i 0 1 2 3 j 0 0 1 2 3 1 1 0 1 2 2 2 1 0 1 3 3 2 1 1