参考：https://mikechen.cc/19178.html

空间复杂度，英文名为Space complexity，是指算法编写成程序后，在计算机中运行时所需存储空间大小的度量。

存储空间一般包括三个方面：

• 输入数据所占用的存储空间；
• 指令常数变量所占用的存储空间；
• 辅助存储空间。

 

一般空间复杂度表示为S(n) = O(f(n))，其中n表示输入规模，fn表示一段程序代码。

 

空间复杂度类型

空间复杂度涉及的空间类型有：

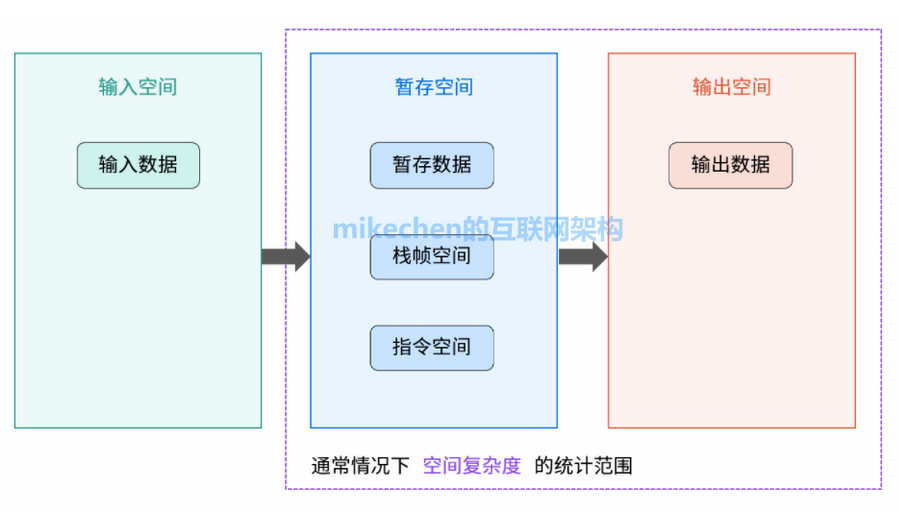
1.输入空间

存储输入数据所需的空间大小；

 

2.暂存空间

算法运行过程中，存储所有中间变量和对象等数据所需的空间大小；

 

3.输出空间

算法运行返回时，存储输出数据所需的空间大小。

通常情况下，空间复杂度指在输入数据大小为 N 时，算法运行所使用的「暂存空间」+「输出空间」的总体大小。

 

常见的空间复杂度？

常见的空间复杂度，如下所示：

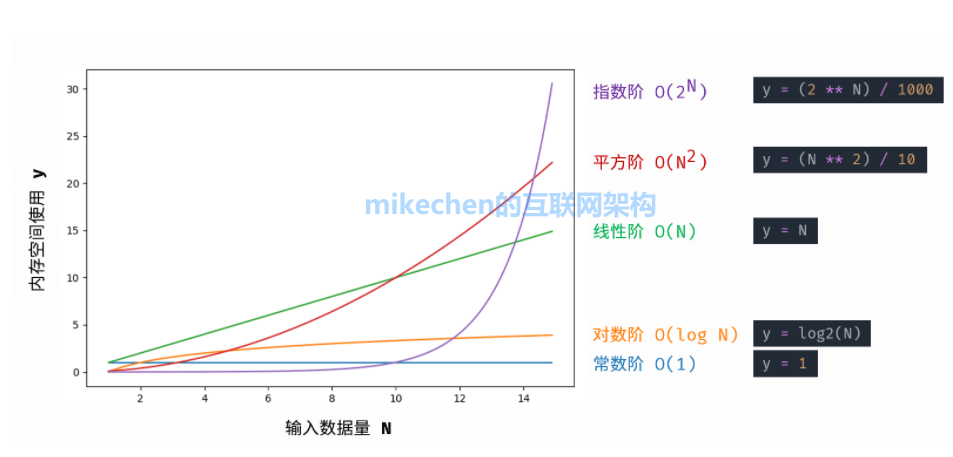
O(1) < O(log N) < O(N) < O(N^2) < O(2^N)

 

上面我们了解了什么是空间复杂度，下面一起来看几个空间复杂度的经典例子，就更清楚了，let’s go!

 

空间复杂度示例

 

1.常数 O(1)

常量空间的意思是该场景空间复杂度和输入规模n无关，那么常量空间的空间复杂度就可以表示O(1)。

比如：普通常量、变量、对象、元素数量与输入数据大小 N 无关的集合，皆使用常数大小的空间。

示例：

int i = 1;
int j = 2;
int m = i + j;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)。

 

2.线性 O(N)

元素数量与 N 呈线性关系的任意类型集合，比如：常见于一维数组、链表、哈希表等，皆使用线性大小的空间。

示例：

int[] m = new int[n]
for(i = 1; i <= n; ++i) {
   j = i;
   j++;
}

这段代码中，第一行new了一个数组出来，这个数据占用的大小为n，后面虽然有循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)。

 

3.平方 O(N^2)

元素数量与 N 呈平方关系的任意类型集合，常见于:矩阵，皆使用平方大小的空间。

示例：

for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
//… }
}

该算法for循环：最外层循环每执行一次，内层循环都要执行n次，执行次数是根据n所决定的，最大时间复杂度是O（n^2），如果内层循环在某种场景一次就跳出,其实也可以退化成o(n)。

 

4.指数 O(2^N)

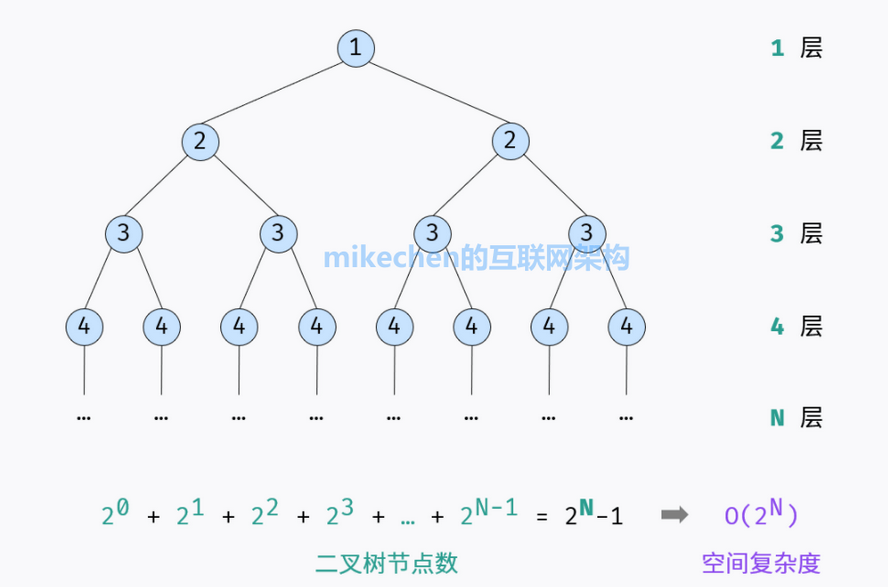
指数阶常见于二叉树、多叉树。例如，高度为 N 的「满二叉树」的节点数量为 2^N，占用 O(2^N) 大小的空间。

同理，高度为 N 的「满 m 叉树」的节点数量为 m^N，占用 O(m^N) = O(2^N) 大小的空间。

 

5.对数 O(logN)

对数阶常出现于分治算法的栈帧空间累计、数据类型转换等。