Alexander Farrugia 的回答:
\(\pi\) 的几何形象可以定义为半径为 \(1\) 个单位的圆的面积。
\({S}={\pi}{r^2}={\pi}\)
\({\pi}^2\) 的几何形象可以定义为管道直径为 \(1\) 个单位喇叭环面的表面积。
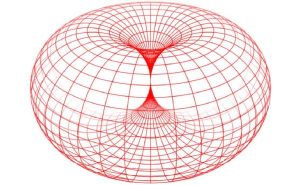
Senia Sheydvasser 的回答:
\({\pi}^2\) 是可计算的。
我们可以利用这个公式:
\({\pi}^2={6}{\sum\limits_{n=1}^{\infty} {\frac{1}{n^2}}}\)
右边的和是所有边长为正整数的正方形面积的倒数和。即:\({1}+{\frac{1}{2^2}}+…+{\frac{1}{n^2}}\)
用 C++ 实现:
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
double sum,tmp1,tmp2; //sum是求和部分的值,tmp1是每轮加给sum的值,tmp2是每次加上tmp1的sum的值。
int n; //n是要求的精确度
cin>>n;
for (double i = 1; i <= n; i++) {
tmp1=1/(i*i);
sum+=tmp1;
tmp2=sum*6
cout << "第" << i << "次精确\t辅助:\t\t\t\t\t\t" << tmp2 << endl;
}
return 0;
}
参考:\({\pi}^2=9.869604401089358618834490999876\)