图论中的一些概念

2022年10月18日 | 分类: 【编程】

原文：https://blog.csdn.net/xsgaaa/article/details/112402374

环

在图论中，环是一条只有第一个和最后一个顶点重复的非空路径。

一个没有环的图被称作无环图。

一个没有有向环的有向图被称做有向无环图。

一个无环的连通图被称作树。

回路，环的定义：

1. 一个回路是一条非空的有向路径，其中第一个顶点和最后一个顶点相同。

概念：空集符号 ∅ 是法国数学家 André Weil 于 1939 年首先采用的，其字形受挪威语和丹麦语字母 Ø 的启发，和希腊字母 Φ 没有关系。汉语读为：空集。英语读为：null set。

令图 $G=(V,E,∅)$ ，
一个回路是一条非空路径 $(e_1,e_2,{\dots},e_n)$ ，
其顶点序列为 $(v_1,v_2,{\dots},v_n,v_1)$ 。

2. 一个环路或简单回路是只有第一个与最后一个顶点相同的回路。

3. 回路和环的长度是它们经过的边的个数。

有向回路，有向环路的定义：

1. 一个有向回路是一个非空的有向路径，其第一个与最后一个顶点相同。

令有向图 $G=(V,E,∅)$ ，
一个回路是一条非空有向路径 $(e_1,e_2,{\dots},e_n)$ ，
其顶点序列为 $(v_1,v_2,{\dots},v_n,v_1)$ 。

2. 一个有向环路，或者简单有向回路，是只有第一个与最后一个顶点重复的有向回路。

自环

在图论中，自环（Loop）是一条顶点与自身连接的边。简单图中不包含自环。

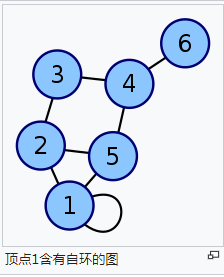
弦

弦在图论里代表连接一个环上不相邻的两个点的一条边。

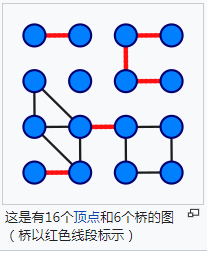
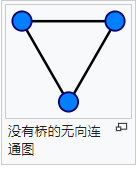
桥 (Bridge)

在图论中，一条边被称为“桥”代表这条边一旦被删除，这张图的连通块数量会增加。

等价地说，一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。

诱导子图（维基百科上叫导出子图）

在图论中，一个图的导出子图(induced subgraph)是指，由该图顶点的一个子集和该图中两端均在该子集的所有边的集合组成的图。

详细定义：

设图 $G=(V,E)$ ，令 $S⊂V$ ，使得 S 是 G 的任意顶点子集。
则G的导出子图 $G[S]$ 中，其顶点集为 S ，边集为 G 的边集 E 中两个顶点均属于S的边的集合。该定义适用于无向图，有向图与多重图。

导出子图 $G[S]$ 也可以称为 S 从 G 中导出的子图，或者（如果上下文中 G 没有歧义）S 的导出子图。

团(clique)

在图论领域的一个无向图中，满足两两之间有边连接的顶点的集合，被称为该无向图的团。团是图论中的基本概念之一，用在很多数学问题以及图的构造上。计算机科学中也有对它的研究，尽管在一个图中寻找给定大小的团达到了NP完全的难度，人们还是研究过很多寻找团的算法。

顶点集C被称为无向图 G=(V,E) 的团（clique），如果C是顶点集V的子集(C⊆V)，而且任意两个C中的顶点都有边连接。另一种等价的说法是，由C诱导的子图是完全图（有时也用“团”来指这样的子图）。

极大团（maximal clique）是指增加任一顶点都不再符合团定义的团，也就是说，极大团不能被任何一个更大的团所包含。

最大团（maximum clique）是一个图中顶点数最多的团。图G的团数（clique number）ω(G) 是指G中最大团的顶点数。图G的边团覆盖数（edge clique cover number）是指覆盖G中所有的边所需要的最少的团的数目。图G的二分维数是指覆盖G中所有边所需要的最少的二分团的数目，其中二分团（biclique）就是完全二分子图。而分团覆盖问题（Clique cover problem）所关心的是用最少的团去覆盖G中所有的顶点。

独立集是刚好和团相反的概念，因为图G中的团和图G的补图中的独立集是一一对应的。

注意：极大团和最大团的英文单词看起来差不多，其实是两个不同的概念。

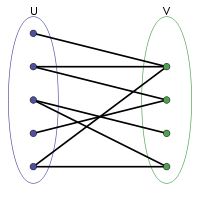
二分图

在图论中，二分图是一类特殊的图，又称为双分图、二部图、偶图。二分图的顶点可以分成两个互斥的独立集 U 和 V 的图，使得所有边都是连结一个 U 中的点和一个 V 中的点。顶点集 U、V 被称为是图的两个部分。等价的，二分图可以被定义成图中所有的环都有偶数个顶点。

连通图

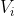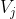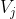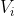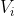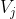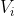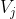作为图论中最基本的概念之一，连通图基于连通的概念。在一个无向图G中，若从顶点 $V_{i}$ 到顶点 $V_{j}$ 有路径相连（当然从 $V_{j}$ 到 $V_{i}$ 也一定有路径），则称 $V_{i}$ 和 $V_{j}$ 是连通的。如果G是有向图，那么连接 $V_{i}$ 和 $V_{j}$ 的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。图的连通性是图的基本性质。连通度是指为了让图分解成孤立的子图所要删除的顶点数的最小值。连通度是刻画网络的一个重要指标。

注意：顶点联通不一定要直接相连，可以通过中间顶点间接相连。

完全图

完全图是一个简单的无向图，其中每一对不同的顶点都只有一条边相连。

完全有向图是一个有向图，其中每一对不同的顶点都只有一对边相连（每个方向各一个）。

注意：这里要求的是两个顶点必须直接相连，可见其要求更高。