参考:https://blog.csdn.net/lan_in/article/details/139151684
参考:https://www.cnblogs.com/Rainy7/p/csp-s-2021-first.html
参考:https://mp.weixin.qq.com/s/WGj-xSb-pYNVioKKrqNS7w
一、单项选择题
(共 15 题,每题 2 分,共计 30 分;每题有且仅有一个正确选项)
【第 1 题】在 Linux 系统终端中,用于列出当前目录下所含的文件和子目录的命令为( )。
A. ls
B. cd
C. cp
D. all
【答案】A
【解析】Linux 系统基础命令。
ls:全拼 list,功能是列出目录的内容及其内容属性信息。
cd:全拼 change directory,功能是从当前工作目录切换到指定的工作目录。
cp:全拼 copy,其功能为复制文件或目录。
all:不存在这个命令。
【第 2 题】二进制数 00101010_2 和 00010110_2的和为( )。
A. 00111100_2
B. 01000000_2
C. 00111100_2
D. 01000010_2
【答案】B
【解析】二进制加法运算。
【第 3 题】在程序运行过程中,如果递归调用的层数过多,可能会由于( )引发错误。
A. 系统分配的栈空间溢出
B. 系统分配的队列空间溢出
C. 系统分配的链表空间溢出
D. 系统分配的堆空间溢出
【答案】A
【解析】递归的时候是像栈一样,先进后出。
由于递归函数的函数信息、参数和局部变量都是存储在系统栈中的,如果递归层数过多,系统分配的栈空间很可能溢出。
【第 4 题】以下排序方法中,( )是不稳定的。
A. 插入排序
B. 冒泡排序
C. 堆排序
D. 归并排序
【答案】C
【解析】堆排序不是相邻元素发生交换。
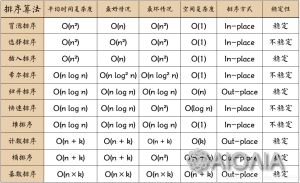
堆排序中原始序列中的任何与顺序相关的信息都在堆的创建阶段丢失了。
比如:3 27 36 27,如果堆顶3先输出,则第三层的27(最后一个27)跑到堆顶,然后堆稳定,然后继续输出堆顶,是刚才这个 27,这样说明后面的 27 先于第二个位置的27 输出,不稳定。
不稳定是什么:
比如 2 个值,第 x 个数字是 z ,第 y 个数值也是 z 。其中不妨设 x < y 。但是某些不稳定的排序后可能会出现 x 排到 y 后面的情况。
【第 5 题】以比较为基本运算,对于 2n 个数,同时找到最大值和最小值,最坏情况下需要的最小的比较次数为( )。
A. 4n−2
B. 3n+1
C. 3n−2
D. 2n+1
【答案】C
【解析1】
\(2+{\frac{2n-2}{2}}\ast3={3n-2}\)
【解析2】
把序列分成两半,长度分别为 n 。两两之间比,小的和最小值比,大的和最大值比。其中两组第一个数只要比一次。
\(1+(n-1)\ast3={3n-2}\)
【解析3】
普通的求最大值是擂台法,选第一个数为当前最大值,将每个数与当前的最大值做比较。如果比当前最大值大就换掉,比当前最大值小就不变,总的比较次数为 2n-1 次。
我们考虑每次选两个数出来,先比较这两个数,两个数中较大的数和当前最大值比较,较小的数和当前最小值比较,除第一次比较完这两个数之后可以直接赋值以外,接下来每两个数只需要进行3次比较,总的比较次数为:
\(1+(\frac{2n}{2}-1)\ast3=3n-2\)
【第 6 题】现有一个地址区间为 0∼10 的哈希表,对于出现冲突情况,会往后找第一个空的地址存储 (到 10 冲突了就从 0 开始往后),现在要依次存储 (0,1,2,3,4,5,6,7),哈希函数为 \(h(x)=x^2 mod 11\) 。请问 7 存储在哈希表哪个地址中( )。
A. 5
B. 6
C. 7
D. 8
【答案】C
【解析1】
每个都算一下。分别为 0,1,4,9,5,3,3,5
重复的调整一下 0,1,4,9,5,3,6,7
【解析2】
第1个数字0对应h(0)=0,因此直接存在0号位置。同样,1存在1号位置,2存在4号位置,3存在9号位置,4存在5号位置(16 mod 11=5),5存在3号位置(25 mod 11=3)。
数字6对应 h(6)=36 mod 11=3,但是3号位置已经有5了,因此从3号往后查找,4、5都有冲突,6存在6号位置。
同样,数字7对应h(7)=49 mod 11=5,5号位置以后第一个空位是7号位置。
【第 7 题】G 是一个非连通简单无向图(没有自环和重边),共有 36 条边,则该图至少有( )个点。
A. 8
B. 9
C. 10
D. 11
【答案】C
【解析1】
9 个顶点的完全无向图有 36 条边,由于非连通,所以再加一个孤立点。
【解析2】
设有 n 个点,除了一个孤立点外剩下点为完全图。
\({\frac{1}{2}}(n−1)(n−2)=36\)
解得 n=10
【解析3】
假设一个非连通简单无向图有 n 个点,那么最多有 (n-1)*(n-2)/2 条边(孤立一个点)。
因此 \(\frac{(n-1)\ast(n-2)}{2}\geq{36}\) 得到 \(n{\geq}{10}\) 。
【第 8 题】令根结点的高度为 1,则一棵含有 2021 个结点的二叉树的高度至少为( )。
A. 10
B. 11
C. 12
D. 2021
【答案】B
【解析1】
“至少”,故是完全二叉树。
\({2^{10}}{\leq}{2021}{\lt}{2^{11}}\)
【解析2】
\(\lvert{{log}_{2}{2021}}\rvert+1=11\)
【解析3】
假设二叉树高度为 \(h\),则这棵树最多有 \(1+2+4+{\dots}+{2^{h-1}}={2^h-1}\) 个点。
由 \({2^h-1}{\geq}2021\) 得 \(h{\geq}11\) 。
【第 9 题】前序遍历和中序遍历相同的二叉树为且仅为( )。
A. 只有 1 个点的二叉树
B. 根结点没有左子树的二叉树
C. 非叶子结点只有左子树的二叉树
D. 非叶子结点只有右子树的二叉树
【答案】D
【解析1】
前序遍历:中左右。
中序遍历:左中右。
所以去掉左时两个相同,选择 D 。
【解析2】
如果树上某个结点A存在左子树B,那么在前序遍历中必然先遍历A,中序遍历中必然先遍历 B,因此出现矛盾。如果不存在这样的结点,则前序遍历和中序遍历完全相同。
【第 10 题】定义一种字符串操作为交换相邻两个字符。将 DACFEB 变为 ABCDEF 最少需要( )次上述操作。
A. 7
B. 8
C. 9
D. 6
【答案】A
【解析】求逆序对个数。
类似冒泡排序,只交换逆序的相邻字母对,共有7个。
考虑冒泡排序思想。
ADCFEB 1 次。
ABDCFE 4 次。
ABCDFE 1 次。
ABCDEF 1 次。
共 7 次。
【第 11 题】有如下递归代码
solve(t, n): if t=1 return 1 else return 5 * solve(t-1, n) mod n
则 solve(23, 23) 的结果为( )。
A. 1
B. 7
C. 12
D. 22
【答案】A
【解析1】
两个函数:`solve` 和 `desolve`,它们分别用于求解代数方程的根和线性常微分方程。
阅读可得,要求\({5^{23-1}}mod{23}\)
考虑用费马小定理,因为 23 是质数,所以:
\({5^{22}}\equiv1(mod{23})\)
故选 A 。
费马小定理:https://oi-wiki.org/math/number-theory/fermat/
【解析2】
\(solve(23, 23)\)
\(= 5*solve(22, 23)\%23\)
\(= 5*5*solve(21, 23)\%23\%23\)
\(= 5*5*5*solve(20, 23)\%23\%23\%23\)
\(= …\)
\(= 5*5*…5*solve(1, 23)\%23\)
\(= 5^22\%23\)
\(=1\)
\({5^{22}}\%{23}={25^{11}}\%{23}={2^{11}}\%{23}=1\)
【第 12 题】斐波那契数列的定义为:
\({F_1}=1,{F_2}=1,{F_n}={{F_{n-1}}+{F_{n-2}}} (n\geq3)\)
现在用如下程序来计算斐波那契数列的第 n 项,其时间复杂度为( )。
F(n): if n<=2 return 1 else return F(n-1) + F(n-2)
A. \(O(n)\)
B. \(O(n^2)\)
C. \(O(2^n)\)
D. \(O(n log{n})\)
【答案】C
【解析1】
T(n)=T(n−1)+T(n−2) ,所以复杂度也是 O(Fn) 。
或者说是 \(2^n\) ,因为每一项都是 Fn=Fn−1+Fn−2 。
故选 C 。
【解析2】
高度为 n 的完全二叉树结点数。
考虑一棵递归树
第1层为 F(n) 总共 1 个结点,
第2层为 F(n-1)、F(n-2) 总共 2 个结点,
第3层为 F(n-2)、F(n-3)、F(n-3)、F(n-4) 总共 4 个结点,
第4层 总共 8 个结点…
以此类推。
由于每层第一个结点比前一层第一个结点少 1,最后因此有 n-1 层。有 \(1+2+4+…+{2^{n-1}}\)。因此时间复杂度为 \(O(2^n)\) 。
【第 13 题】有 8 个苹果从左到右排成一排,你要从中挑选至少一个苹果,并且不能同时挑选相邻的两个苹果,一共有( )种方案。
A. 36
B. 48
C. 54
D. 64
【答案】C
【解析1】枚举法。
选 1 个苹果,有 8 种结果。
选 2 个苹果,可以固定第一个往后,有 6+5+4+3+2+1=21 种。
选 3 个苹果,有 4+3+2+1+3+2+1+2+1+1=20 种。
选 4 个苹果,有 5 种。
所以总数 8+21+20+5=54
【解析2】递推法。
设f(n)为前n个苹果,必选第n个苹果,并且不同时选相邻苹果的方案数。
f(1)=1
f(2)=1
f(3)=f(1)+1=2
f(4)=f(1)+f(2)+1=3
f(5)=f(1)+f(2)+f(3)+1=5
f(6)=f(1)+f(2)+f(3)+f(4)+1=8
f(7)=f(1)+f(2)+f(3)+f(4)+f(5)+1=13
f(8)=f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+1=21
最终的答案为:f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)+f(8)=54。
【第 14 题】设一个三位数 \(n=\overline{abc}\) ,a,b,c 均为 1∼9 之间的整数,若以 a、b、c 作为三角形的三条边可以构成等腰三角形(包括等边),则这样的 n 有( )个。
A. 81
B. 120
C. 165
D. 216
【答案】C
【解析1】
可选数字有:
111,
221,222,223
331,332,333,334 335
441,442,443,444,445,446,447
551,552,553 554,555,556,557,558,559
…
其中三数相等的有9个,AAB 式的有 2+4+6+8*5=52个,每个 AAB 式的可以形成3个数。
因此答案为 9+52*3=165
【解析2】
考虑 a=b≠c 有几种。
1,1 无解。
2,2 有 2+2−1−1=2 种。
3,3 有 4 种。
4,4 有 6 种。
后面 5 到 9 都是 8 种。
所以 8×5+6+4+2=52
而 a=b=c 有 9 种。
所以 52×3+9=165 种。
故选 C 。
【第 15 题】有如下的有向图,节点为 A,B,⋯,J,其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为( )。
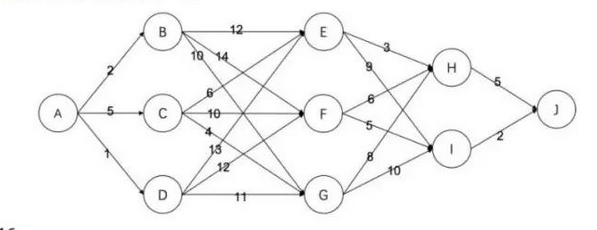
A. 16
B. 19
C. 20
D. 22
【答案】B
【解析1】
可以分层求出最短路,得到最短路径为\({A}\to{C}\to{E}\to{H}\to{J}\)
【解析2】
模拟 Dijkstra 算法过程。
二、阅读程序
(程序输入不超过数组或字符串定义的范围;判断题正确填 √ ,错误填 × ;除特 殊说明外,判断题 1.5分,选择题 3 分,共计 40 分)
阅读程序1
#include <iostream>
#include <cmath>
using namespace std;
const double r = acos(0.5);
int a1, b1, c1, d1;
int a2, b2, c2, d2;
inline int sq(const int x) { return x * x; }
inline int cu(const int x) { return x * x * x; }
int main()
{
cout.flags(ios::fixed);
cout.precision(4);
cin >> a1 >> b1 >> c1 >> d1;
cin >> a2 >> b2 >> c2 >> d2;
int t = sq(a1 - a2) + sq(b1 - b2) + sq(c1 - c2);
if(t <= sq(d2 - d1)) cout << cu(min(d1, d2)) * r * 4;
else if(t >= sq(d1 + d2)) cout << 0;
else{
double x = d1 - (sq(d1) - sq(d2) + t) / sqrt(t) / 2;
double y = d2 - (sq(d2) - sq(d1) + t) / sqrt(t) / 2;
cout << (x * x * (3 * d1 - x) + y * y * (3 * d2 - y)) * r;
}
cout << endl;
return 0;
}
假设输入的所有数的绝对值都不超过 1000 ,完成下面的判断题和单选题:
【程序分析】求两个球的体积的交,注
π
。
-
判断题
16、 将第 21 行中 t 的类型声明从 int 改为 double, 不会 影响程序运行的结果。( )
【解析】sq 返回值为 int 类型。
【答案】T
17、将第 26、27 行中的 / sqrt(t) / 2 替换为 / 2 / sqrt(t),不会影响程序运行的结果。( )
【解析】先除以 2 可能会造成整除丢失数据。
【答案】F
18、 将第 28 行中的 x * x 改成 sq(x)、y * y 改成 sq(y),不会影响程序运行的结果。( )
【解析】sq 函数的参数为 int 类型。
【答案】F
19、(2 分) 当输入为 0 0 0 1 1 0 0 1 时,输出为1.3090( )
【解析】两个半径为 1 的球的体积的交。
【答案】T
-
单选题
20、当输入为 1 1 1 1 1 1 1 2 时,输出为( )。
A. 3.1416
B. 6.2832
C. 4.7124
D. 4.1888
【解析】同心球,计算小球的体积。
【答案】D
21、(2.5 分)这段代码的含义为( )。
A. 求圆的面积并
B. 求球的体积并
C. 求球的体积交
D. 求椭球的体积并
【解析】由 23-29 行选择结构进行判断。
【答案】C
阅读程序2
#include <algorithm>
#include <iostream>
using namespace std;
int n, a[1005];
struct Node
{
int h, j, m, w;
Node(const int _h, const int _j, const int _m, const int _w) :
h(_h), j(_j), m(_m), w(_w)
{}
Node operator+(const Node &o) const
{
return Node(
max(h, w + o.h),
max(max(j, o.j), m + o.h),
max(m + o.w, o.m),
w + o.w);
}
};
Node solve1(int h, int m)
{
if(h > m)
return Node(-1, -1, -1, -1);
if(h == m)
return Node(max(a[h], 0), max(a[h], 0), max(a[h], 0), a[h]);
int j = (h + m) >> 1;
return solve1(h, j) + solve1(j + 1, m);
}
int solve2(int h, int m)
{
if(h > m)
return -1;
if(h == m)
return max(a[h], 0);
int j = (j + m) >> 1;
int wh = 0, wm = 0;
int wht = 0, wmt = 0;
for(int i = j; i >= h; i--){
wht += a[i];
wh = max(wh, wht);
}
for(int i = j + 1; i <= m; i++){
wmt += a[i];
wm = max(wm, wmt);
}
return max(max(solve2(h, j), solve2(j + 1, m)), wh + wm);
}
int main() {
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
cout << solve1(1, n).j << endl;
cout << solve2(1, n) << endl;
return 0;
}
假设输入的所有数的绝对值都不超过 1000 ,完成下面的判断题和单选题:
-
判断题
22、程序总是会正常执行并输出两行两个相等的数。( )
【解析】solve1 和 solve2 都是求最大连续子段和。
【答案】T
23、 第 28 行与第 38 行分别有可能执行两次及以上。( )
【解析】函数返回条件只执行一次。
【答案】F
24、 当输入为 5 -10 11 -9 5 -7 时,输出的第二行为 7。( )
【解析】最大连续子段和为 11。
【答案】F
单选题
25、solve1(1, n) 的时间复杂度为( )。
A.
B.
C.
D.
【解析】
。
【答案】B
26、solve2(1, n) 的时间复杂度为( )。
A.
B.
C.
D.
【解析】
。
【答案】C
27、当输入为 10 -3 2 10 0 -8 9 -4 -5 9 4 时,输出的第一行为( )。
A. 13
B. 17
C. 24
D. 12
【解析】2+10+0-8+9-4-5+9+4=17。
【答案】B
阅读程序3
#include <iostream>
#include <string>
using namespace std;
char base[64];
char table[256];
void init()
{
for(int i = 0; i < 26; i++) base[i] = 'A' + i;
for(int i = 0; i < 26; i++) base[26 + i] = 'a' + i;
for(int i = 0; i < 10; i++) base[52 + i] = '0' + i;
base[62] = '+', base[63] = '/';
for(int i = 0; i < 256; i++) table[i] = 0xff;
for(int i = 0; i < 64; i++) table[base[i]] = i;
table['='] = 0;
}
string encode(string str)
{
string ret;
int i;
for(int i = 0; i + 3 <= str.size(); i += 3){
ret += base[str[i] >> 2];
ret += base[(str[i] & 0x03) << 4 | str[i + 1] >> 4];
ret += base[(str[i] & 0x0f) << 2 | str[i + 2] >> 6];
ret += base[str[i + 2] & 0x3f];
}
if(i < str.size()){
ret += base[str[i] >> 2];
if(i + 1 == str.size()){
ret += base[(str[i] & 0x03) << 4];
ret += "==";
}
else{
ret += base[(str[i] & 0x03) << 4 | str[i + 1] >> 4];
ret += base[(str[i] & 0x0f) << 2];
ret += "=";
}
}
return ret;
}
string decode(string str)
{
string ret;
int i;
for(int i = 0; i < str.size(); i += 4){
ret += table[str[i]] << 2 | table[str[i + 1]] >> 4;
if(str[i + 2] != '=')
ret += (table[str[i + 1]] & 0x0f) << 4 | table[str[i + 2]] >> 2;
if(str[i + 3] != '=')
ret += table[str[i + 2]] << 6 | table[str[i + 3]];
}
return ret;
}
int main()
{
init();
cout << int(table[0]) << endl;
int opt;
string str;
cin >> opt >> str;
cout << (opt ? decode(str) : encode(str)) << endl;
return 0;
}
假设输入总是合法的(一个整数和一个不含空白字符的字符串,用空格隔开),完成下面的判断题和单选题:
【注】该题目与 CSP-J 2021 题目一个分析思路,仅仅是多了 enode 函数。
-
判断题
28、程序总是先输出 一行 一个整数,再输出 一行 一个字符串。( )
【解析】输出可能会出现换行符。
【答案】F
29、 对于任意不含空白字符的字符串 str1,先执行程序输入 0 str1,得到输出的第二行记为 str2 再执行程序输入 1 str2,输出的第二行必为 str1。( )
【解析】加密解密操作。
【答案】T
30、 当输入为 1 SGVsbG93b3JsZA== 时,输出的第二行为 HelloWorld。( )
【解析】输出 Helloworld。
【答案】F
-
单选题
31、设输入字符串长度为 n,encode 函数的时间复杂度为( )。
A.
B.
C.
D.
【解析】与字符串长度正相关。
【答案】B
32、输出的第一行为( )。
A. 0xff
B. 255
C. 0xFF
D. -1
【解析】-1 的补码在内存中都是 1。
【答案】D
33、(4 分) 当输入为 0 CSP2021csp 时,输出的第二行为( )。
A. Q1NQMjAyMWNzcAv=
B. Q1NQMjAyMGNzcA==
C. Q1NQMjAyMGNzcAv=
D. Q1NQMjAyMWNzcA==
【解析】代入计算。
【答案】D
三、完善程序
(单选题,每小题 3 分,共计 30 分)
完善程序1

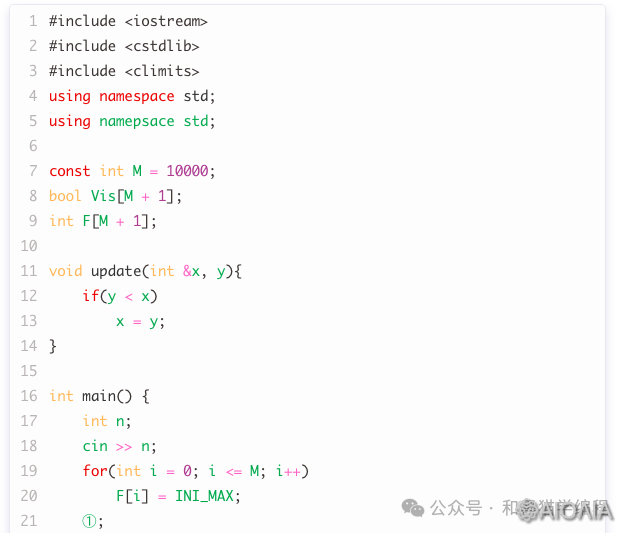

-
① 处应填( )。
A. F[4] = 0
B. F[1] = 4
C. F[1] = 2
D. F[4] = 1
【解析】初始值:4 只需要 1 个 4 组成。
【答案】D
-
② 处应填( )。
A. !Vis[n]
B. r < n
C. F[M] == INT_MAX
D. F[n] == INT_MAX
【解析】当 n 没有被计算过才执行循环。
【答案】A
-
③ 处应填( )。
A. F[i] == r
B. !Vis[i] && F[i] == r
C. F[i] < F[x]
D. !Vis[i] && F[i] < F[x]
【解析】找到没有被计算过的 i 中,F[i] 最小的一个。
【答案】D
-
④ 处应填( )。
A. F[i] < F[x]
B. F[i]<=r
C. Vis[i]
D. i <= x
【解析】i 和 x 都是确定的,再通过组合计算出新的数字最少可以由多少个 4 组成。
【答案】C
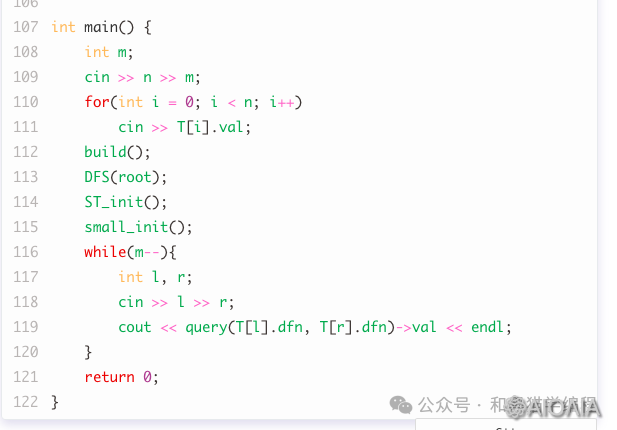
完善程序2





-
① 处应填( )。
A. p->son[0] = S[top–]
B. p->son[1] = S[top–]
C. S[top–]->son[0] = p
D. S[top–]->son[1] = p
【解析】笛卡尔树,大根堆,维护单调递增栈。
【答案】A
-
② 处应填( )。
A. p->son[0] = S[top]
B. p->son[1] = S[top]
C. S[top]->son[0] = p
D. S[top]->son[1] = p
【解析】将 p 放到 右孩子位置。
【答案】D
-
③ 处应填( )。
A. x->dep < y->dep
B. x < y
C. x->dep > y->dep
D. x->val < y->val
【解析】LCA 找层数最小的。
【答案】A
-
④ 处应填( )。
A. A[i * b + j – 1] == A[i * b + j]->son[0]
B. A[i * b + j]->val < A[i * b + j – 1]->val
C. A[i * b + j] == A[i * b + j – 1]->son[1]
D. A[i * b + j]->dep < A[i * b + j – 1]->dep
【解析】当前深度比上第一个深度小为 1,否则为 0。
【答案】D
-
⑤ 处应填( )。
A. v += (S >> i & 1) ? -1 : 1
B. v += (S >> i & 1) ? 1 : -1
C. v += (S >> (i – 1) & 1) ? 1 : -1
D. v += (S >> (i – 1) & 1) ? -1 : 1
【解析】v 是最小层数。
【答案】D
-
⑥ 处应填( )
A. (Dif[p] >> (r – p * b)) & ((1 << (r – l)) – 1)
B. Dif[p]
C. (Dif[p] >> (l – p * b)) & ((1 << (r – l)) – 1)
D. (Dif[p] >> ((p + 1) * b – r)) & ((1 << (r – l + 1)) – 1)
【解析】右侧对齐。
【答案】C