2022年CSP-J-初赛试卷及解析
2024年7月6日 | 分类: 【编程】
参考:https://blog.csdn.net/lq1990717/article/details/126971665
参考:https://www.cnblogs.com/hellohebin/p/16709315.html
一、单项选择题(共 15 题,每题 2 分,共计 30 分;每题有且仅有一个正确选项)
1. 以下哪种功能没有涉及 C++ 语言的面向对象特性支持:( )。
A. C++ 中调用 printf 函数
B. C++ 中调用用户定义的类成员函数
C. C++ 中构造一个 class 或 struct
D. C++ 中构造来源于同一基类的多个派生类
答案:A。
解析:
printf是C语言中就可以使用的函数
而c++中定义类或结构体,对象调用成员函数,构造派生类,都是面向对象语言才能支持的操作。
面向对象(oritend-object,OO):以问题根源作为关注点:人,饭
面向过程(oritend-process,OP):以问题本身作为关注点:吃饭
printf是C语言中的一个输出函数,并不涉及到OOP特性,只要涉及到类(class)都是属于OOP特性。
面向对象编程中具有的三大特性:
封装:隐藏对象的属性和实现细节,仅对外提供公共访问方式。
继承:将可复用的类作为基类(父类),子类继承父类,提高代码复用性。
多态:父类或接口定义的引用变量可以指向子类或具体实现类的实例对象。
2. 有 6 个元素,按照 6 、 5 、 4 、 3 、 2 、 1 的顺序进入栈 S ,请问下列哪个出栈序列是非法的( )。
A. 5 4 3 6 1 2
B. 4 5 3 1 2 6
C. 3 4 6 5 2 1
D. 2 3 4 1 5 6
答案:C。
解析:入栈出栈序列问题,
如果数值a出栈,那么在a前入栈的元素要么已出栈,要么顺序地排列在栈中。
C选项中,当4出栈时,4前入栈的6,5一定都在栈中,情况为:栈底-6-5。所以接下来不可能是6出栈,只能是5出栈。
栈:后进先出表(LIFO)
找规律:入栈降序序,出栈如果降序或者连续升序合法;当陡升时,元素应当为栈内最小值,四个选项中陡升情况如下。
A. 5 4 [3 6] 1 2;其中6是栈内最小值,合法。
B. 4 5 3 1 2 6
C. 3 [4 6] 5 2 1;其中6不是栈内最小值,应当为5。
D. 2 3 4 1 5 6
3. 运行以下代码片段的行为是( )。
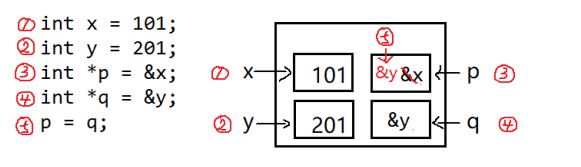
int x = 101;
int y = 201;
int *p = &x;
int *q = &y;
p = q;
A. 将 x 的值赋为 201
B. 将 y 的值赋为 101
C. 将 q 指向 x 的地址
D. 将 p 指向 y 的地址
答案:D。
解析:
p是指向x的指针,也就是x的地址。
q是指向y的指针,也就是y的地址。
把q赋值给p,也就是让p从指向x的指针变为指向y的指针。
4. 链表和数组的区别包括( )。
A. 数组不能排序,链表可以
B. 链表比数组能存储更多的信息
C. 数组大小固定,链表大小可动态调整
D. 以上均正确
答案:C。
解析:
选项A:数组和链表都能做排序。比如冒泡排序,里面只有交换相邻元素的操作,这一操作在数组和链表中都可以做。
选项B:链表和数组能存储的信息取决于其长度,哪个更长哪个能存储更多信息。
C选项是正确的。一旦申请数组,数组的长度就是固定的了。而链表可以申请和释放结点,大小可以动态调整。
A. 错误;sort排序用的那么多,肯定错的,数组可以排序,链表可以排序;
理论上,任何数据结构都是可以规定其先后的,也就是排序。
B. 正确;链表比数组能存储更多的信息,我们说引入链表的原因就是因为数组的空间是连续的,而要开辟一段连续的很大的内存空间是不行的,于是可以开辟不连续的内存空间(节点),通过指针来连接各个空间,从而构建了链表。那么说链表比数组能存储更多的信息是正确的。
C. 正确;有人会说vector动态数组可以调整大小,C就错误了。但其实vector的本质是当数组a容量不够时,新建数组b并复制数组a的内容到b,之后销毁a,数组a,b本身的长度是固定的。
链表大小是通过节点数量确定的,而节点数量是可以变化的,所以链表大小可动态调整。
那么问题来说,答案不就选BC了吗?怎么多选了?
其实笔者认为题目稍微有点小问题,如果我是出题人,肯定会给BC都正确。
但是对于B.链表比数组能存储更多的信息,是具有一定的限制条件的,你可以试想一下,一个电脑内存设置空间大小刚好为可开长度为 N 的数组,并且内存已经开辟完了,那么如果使用链表,而链表是需要指针域来占用空间的,所以相比之下,数组的存储空间更大了。
所以建议加上限定条件:当内存一定时,….
5. 对假设栈 S 和队列 Q 的初始状态为空。存在 e1~e6 六个互不相同的数据,每个数据按照进栈 S 、出栈 S 、进队列 Q 、出队列 Q 的顺序操作,不同数据间的操作可能会交错。已知栈 S 中依次有数据 e1 、 e2 、 e3 、 e4 、 e5 和 e6 进栈,队列 Q 依次有数据 e2 、 e4 、 e3 、e6 、 e5 和 e1 出队列。则栈 S 的容量至少是( )个数据。
A. 2
B. 3
C. 4
D. 6
答案:B。
解析:
栈是后进先出,队列是先进先出。
队列出队的顺序,就是队列入队的顺序。而队列入队的顺序,就是栈出栈的顺序。所以该题变为:
已知入栈顺序是:e1,e2,e3,e4,e5,e6,出栈顺序是:e2,e4,e3,e6,e5,e1,请问在整个入栈出栈过程中栈中元素的最大个数。
根据入栈出栈顺序,可知:
| 操作 |
栈内情况(左侧是栈底) |
出栈序列 |
| e1入栈 |
e1 |
|
| e2入栈 |
e1,e2 |
|
| e2出栈 |
e1 |
e2 |
| e3入栈 |
e1,e3 |
e2 |
| e4入栈 |
e1,e3,e4 |
e2 |
| e4出栈 |
e1,e3 |
e2,e4 |
| e3出栈 |
e1 |
e2,e4,e3 |
| e5入栈 |
e1,e5 |
e2,e4,e3 |
| e6入栈 |
e1,e5,e6 |
e2,e4,e3 |
| e6出栈 |
e1,e5 |
e2,e4,e3,e6 |
| e5出栈 |
e1 |
e2,e4,e3,e6,e5 |
| e1出栈 |
|
e2,e4,e3,e6,e5,e1 |
根据上表可知栈中最大元素数量为3。

6. 对表达式 a+(b-c)*d 的前缀表达式为( ),其中 + 、 – 、 * 是运算符。
A. *+a-bcd
B. +a*-bcd
C. abc-d*+
D. abc-+d
答案:B。
解析:
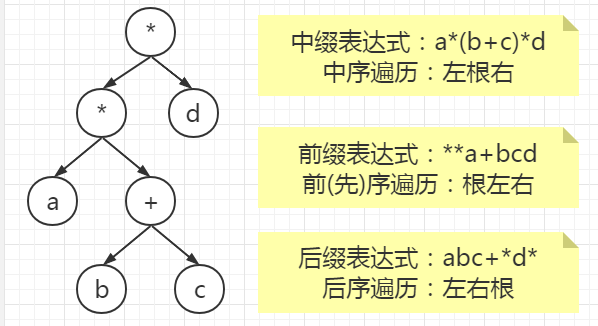
中缀表达式转前缀表达式。先运算b-c,变为-bc。然后是X*d(X为b-c),变为*Xd。把X的前缀表达式代入,为*-bcd。最后是a+X(X为(b-c)*d),变为+aX,把X的前缀表达式代入,为+a*-bcd。
中缀表达式:a+b、前缀表达式:+ab、后缀表达式:ab+。
对于这个问题,我们可以将其中的某一部分看作一个整体,如 a+(b-c)*d 中(b-c)应当为一个数 x,所以对其变前缀就是 x=(-bc)。
原式就变为 a+x*d -> a+(*xd) -> +a(*xd) -> +a*-bcd。
这里可以结合二叉树的遍历方式一起回忆。
7. 假设字母表 {a, b, c, d, e} 在字符串出现的频率分别为 10%, 15%, 30%, 16%,29% 。若使用哈夫曼编码方式对字母进行不定长的二进制编码,字母 d 的编码长度为( )位。
A. 1
B. 2
C. 2 或 3
D. 3
答案:B
【解析1】:
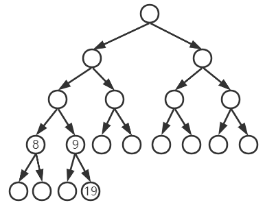
考察哈夫曼树和哈夫曼编码。构建哈夫曼树的方法为:每次选取两个权值最小的结点,加上双亲结点构成一棵树。
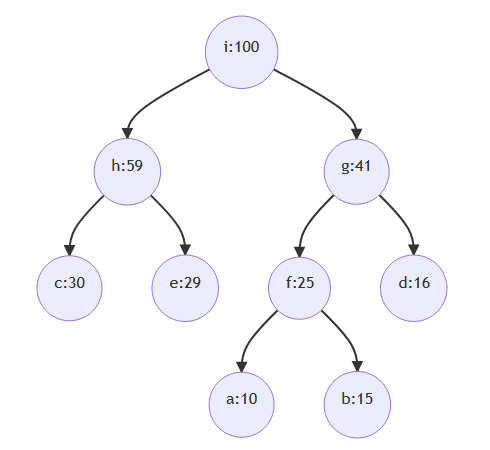
初始一共有5个结点,每个结点的权值分别为:a:10,b:15,c:30,d:16,e:29
选择权值最小的两个结点a和b,设结点f是a、b的双亲,权值25。
选择权值最小的两个结点f和d,设结点g是f、d的双亲,权值41。
选择权值最小的两个结点c和e,设结点h是c、e的双亲,权值59。
选择权值最小的两个结点g和h,设结点i是g、h的双亲,权值100。
构成的树如下图所示。
在哈夫曼树中,从根结点开始,每向下走一层编码多1位。根据构造出来的哈夫曼树可知,d的编码是两位。
【解析2】
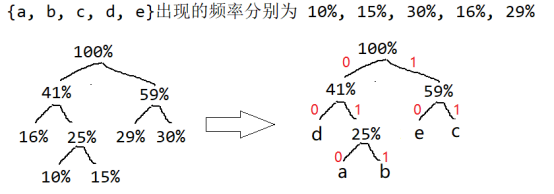
哈夫曼编码基于信源的概率统计模型,它的基本思路是出现概率大的信源符号编短码,出现概率小的信源符号编长码,从而使平均码长最小。这是一种贪心策略,每次选取当前概率最大的符号使用现有的最短码。
构建:选择最小权值与次小权值组成一棵树,最小在左,并将其加入集合。
编码:规定哈夫曼树中的左分支为0,右分支为1,则从根结点到每个叶结点所经过的分支对应的 0和 1组成的序列便为该结点对应字符的编码。
8. 一棵有 n 个结点的完全二叉树用数组进行存储与表示,已知根结点存储在数组的第 1 个位置。若存储在数组第9个位置的结点存在兄弟结点和两个子结点,则它的兄弟结点和右子结点的位置分别是( )。
A. 8 、 18
B. 10 、 18
C. 8 、 19
D. 10 、 19
答案:C
解析:
二叉树的顺序存储结构中,第i结点的左孩子的下标为2*i,右孩子的下标为2*i+1,双亲的下
标为i/2。
因此第9位置结点一定是第4结点的右孩子(左孩子下标都是偶数,右孩子下标都是奇数)。
该结点的兄弟结点是4的左孩子,在数组中的下标应该比9少1,为8。
9的右孩子的下标为 9*2+1=19。
9. 考虑由N个顶点构成的有向连通图,采用邻接矩阵的数据结构表示时,该矩阵中至少存在( )个非零元素。
A. N-1
B. N
C. N+1
D. N^2
答案:A。
解析:
有向连通图,分为强连通图、单向连通图、弱连通图。若把有向边都当做无向边,如果这个无向图是连通图,那么这个图是弱连通图。
n个顶点的无向图,最少有n-1条边。那么这个有向图中最少有n-1条边,就可以构成弱连通图。有向图中每条边在邻接矩阵中就是一个元素,占一个位置,因此至少存在n-1个非零元素。
答案:B
解析:笔者认为描述不明确(权值无明确初始值,有向连通图表述不清楚)。
若从顶点 i 到顶点 j 有路径,则称顶点 i 和 j 是连通的。
若无向图 G 中任意两个顶点都连通,则称为连通图,否则称为非连通图。
若有向图 G 中任意两个顶点都连通,则称为强连通图。
有向图 G 中的极大强连通子图称为 G 的强连通分量。
思路:构造一个 N 个点的有向连通图,一个圆环 N 条边。
但是还没有加 a[i][i]=1 和特判 N=1 的情况,我认为这个题目有争议!
10. 以下对数据结构的表述不恰当的一项为:( )。
A. 图的深度优先遍历算法常使用的数据结构为栈。
B. 栈的访问原则为后进先出,队列的访问原则是先进先出。
C. 队列常常被用于广度优先搜索算法。
D. 栈与队列存在本质不同,无法用栈实现队列。
答案:D
解析:
选项A:图的深度优先遍历算法经常用递归来完成,而递归实际是利用了C++中的函数递归调用栈,本质上是使用了栈的结构。实际上,如果直接使用栈,也可以完成图的深度优先遍历。
选项B、C都是正确的表述。
选项D中,栈与队列本质上都是功能受限的线性表,本质是相同的。用栈实现队列,虽然平时不会这样做,这样做也没什么意义,但还是可以实现的。
设栈s1与s2来实现一个队列的功能:
入队:元素入栈s1
出队:如果栈s2不为空,那么栈s2出栈。如果s2为空,那么把s1中的所有元素出栈并入栈到s2,而后s2出栈。
11. 以下哪组操作能完成在双向循环链表结点 p 之后插入结点 s 的效果(其中, next 域为结点的直接后继, prev 域为结点的直接前驱):( )。
A. p->next->prev=s; s->prev=p; p->next=s; s->next=p->next;
B. p->next->prev=s; p->next=s; s->prev=p; s->next=p->next;
C. s->prev=p; s->next=p->next; p->next=s; p->next->prev=s;
D. s->next=p->next; p->next->prev=s; s->prev=p; p->next=s;
答案:D。
解析:
观察选项可知,四个选项为这四个语句的不同排列:
s->prev=p;
s->next=p->next;
p->next=s;
p->next->prev=s;
这里发生变化,又可能给其它量赋值的就是p->next。
使p->next发生变化的语句为:p->next=s;
而s->next=p->next;与p->next->prev=s;中用到的都应该是变化前的p->next,指向的是原来p的下一个结点。
所以p->next=s;应该放在最后,选D。
12. 以下排序算法的常见实现中,哪个选项的说法是错误的:( )。
A. 冒泡排序算法是稳定的
B. 简单选择排序是稳定的
C. 简单插入排序是稳定的
D. 归并排序算法是稳定的
答案:B
解析:
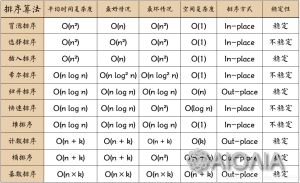
考察排序的稳定性。选择排序是不稳定的,冒泡、插入、归并都是稳定的。
算法大全:
13. 八进制数 32.1 对应的十进制数是( )。
A. 24.125
B. 24.250
C. 26.125
D. 26.250
答案:C
解析:
进制转换问题,八进制转十进制的方法为:按位权展开。
整数部分: \({3}\ast{8^1}+{2}\ast{8^0}=26\)
小数部分: \({1}\ast{8^{-1}}=0.125\)
因此八进制 32.1 为十进制 26.125 ,选C。
14. 一个字符串中任意个连续的字符组成的子序列称为该字符串的子串,则字符串 abcab 有( )个内容互不相同的子串。
A. 12
B. 13
C. 14
D. 15
答案:B。
解析:
abcab的不相同子串有:
长为0的子串:空串
长为1的子串:a,b,c
长为2的子串:ab,bc,ca
长为3的子串:abc,bca,cab
长为4的子串:abca,bcab
长为5的子串:abcab
共有13个。
15. 以下对递归方法的描述中,正确的是:( )
A. 递归是允许使用多组参数调用函数的编程技术
B. 递归是通过调用自身来求解问题的编程技术
C. 递归是面向对象和数据而不是功能和逻辑的编程语言模型
D. 递归是将用某种高级语言转换为机器代码的编程技术
答案:B。
解析:
选项A:不清楚什么叫“多组参数调用函数”,任意一个带参函数,都可以用多组参数来调用。
选项B:论述正确。
选项C:面向对象编程(或者说“类”)是面向对象和数据而不是功能和逻辑的编程语言模型。
选项D:编译是将用某种高级语言转换为机器代码的编程技术
二、阅读程序
(程序输入不超过数组或字符串定义的范围;判断题正确填√,错误填×;除特殊说明外,判断题 1.5 分,选择题 3 分,共计 40 分)
(1) 第16-21题
#include <iostream>
using namespace std;
int main()
{
unsigned short x, y;
cin >> x >> y;
x = (x | x << 2) & 0x33;
x = (x | x << 1) & 0x55;
y = (y | y << 2) & 0x33;
y = (y | y << 1) & 0x55;
unsigned short z = x | y << 1;
cout << z << endl;
return 0;
}
判断题
16. 删去第 7 行与第 13 行的 unsigned ,程序行为不变。( )
17. 将第 7 行与第 13 行的 short 均改为 char ,程序行为不变。( )
18. 程序总是输出一个整数“ 0 ”。( )
19. 当输入为“ 2 2 ”时,输出为“ 10 ”。( )
20. 当输入为“ 2 2 ”时,输出为“ 59 ”。( )
单选题
21. 当输入为“ 13 8 ”时,输出为( )。
A. “ 0 ”
B. “ 209 ”
C. “ 197 ”
D. “ 226 ”
(2) 第22-27题
#include <algorithm>
#include <iostream>
#include <limits>
using namespace std;
const int MAXN = 105;
const int MAXK = 105;
int h[MAXN][MAXK];
int f(int n, int m)
{
if (m == 1) return n;
if (n == 0) return 0;
int ret = numeric_limits<int>::max();
for (int i = 1; i <= n; i++)
ret = min(ret, max(f(n - i, m), f(i - 1, m - 1)) + 1);
return ret;
}
int g(int n, int m)
{
for (int i = 1; i <= n; i++)
h[i][1] = i;
for (int j = 1; j <= m; j++)
h[0][j] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= m; j++) {
h[i][j] = numeric_limits<int>::max();
for (int k = 1; k <= i; k++)
h[i][j] = min(
h[i][j],
max(h[i - k][j], h[k - 1][j - 1]) + 1);
}
}
return h[n][m];
}
int main()
{
int n, m;
cin >> n >> m;
cout << f(n, m) << endl << g(n, m) << endl;
return 0;
}
(3) 第28-34题
#include <iostream>
using namespace std;
int n, k;
int solve1()
{
int l = 0, r = n;
while (l <= r) {
int mid = (l + r) / 2;
if (mid * mid <= n) l = mid + 1;
else r = mid - 1;
}
return l - 1;
}
double solve2(double x)
{
if (x == 0) return x;
for (int i = 0; i < k; i++)
x = (x + n / x) / 2;
return x;
}
int main()
{
cin >> n >> k;
double ans = solve2(solve1());
cout << ans << ' ' << (ans * ans == n) << endl;
return 0;
}
三、完善程序
(1) 第35-39题
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> fac;
fac.reserve((int)ceil(sqrt(n)));
int i;
for (i = 1; i * i < n; ++i) {
if (①) {
fac.push_back(i);
}
}
for (int k = 0; k < fac.size(); ++k) {
cout << ② << " ";
}
if (③) {
cout << ④ << " ";
}
for (int k = fac.size() - 1; k >= 0; --k) {
cout << ⑤ << " ";
}
}
(2) 第40-44题
#include <bits/stdc++.h>
using namespace std;
const int ROWS = 8;
const int COLS = 8;
struct Point {
int r, c;
Point(int r, int c) : r(r), c(c) {}
};
bool is_valid(char image[ROWS][COLS], Point pt,
int prev_color, int new_color) {
int r = pt.r;
int c = pt.c;
return (0 <= r && r < ROWS && 0 <= c && c < COLS &&
① && image[r][c] != new_color);
}
void flood_fill(char image[ROWS][COLS], Point cur, int new_color) {
queue<Point> queue;
queue.push(cur);
int prev_color = image[cur.r][cur.c];
②;
while (!queue.empty()) {
Point pt = queue.front();
queue.pop();
Point points[4] = {③, Point(pt.r - 1, pt.c),
Point(pt.r, pt.c + 1), Point(pt.r, pt.c - 1)};
for (auto p : points) {
if (is_valid(image, p, prev_color, new_color)) {
④;
⑤;
}
}
}
}
int main() {
char image[ROWS][COLS] = {{'g', 'g', 'g', 'g', 'g', 'g', 'g', 'g'},
{'g', 'g', 'g', 'g', 'g', 'g', 'r', 'r'},
{'g', 'r', 'r', 'g', 'g', 'r', 'g', 'g'},
{'g', 'b', 'b', 'b', 'b', 'r', 'g', 'r'},
{'g', 'g', 'g', 'b', 'b', 'r', 'g', 'r'},
{'g', 'g', 'g', 'b', 'b', 'b', 'b', 'r'},
{'g', 'g', 'g', 'g', 'g', 'b', 'g', 'g'},
{'g', 'g', 'g', 'g', 'g', 'b', 'b', 'g'}};
Point cur(4, 4);
char new_color = 'y';
flood_fill(image, cur, new_color);
for (int r = 0; r < ROWS; r++) {
for (int c = 0; c < COLS; c++) {
cout << image[r][c] << " ";
}
cout << endl;
}
// 输出:
// g g g g g g g g
// g g g g g g r r
// g r r g g r g g
// g y y y y r g r
// g g g y y r g r
// g g g y y y y r
// g g g g g y g g
// g g g g g y y g
return 0;
}






