参考:https://blog.csdn.net/jinjiayang/article/details/133412967
参考:https://blog.csdn.net/guolianggsta/article/details/133621608
参考:https://www.cnblogs.com/hellohebin/p/17797499.html
暴露问题
1. T1,T4 很多 MLE,数组开大了,同学们要学习计算空间大小,不要盲开.
2. T1 有很多递归实现的,int无返回值.
3. T2 局部变量未初始化,O2优化后会出现问题.
4. T3 sqrt写成sprt, gcd写的暴力.
5. 文件保存位置不对,导致没有收取到选手文件
6. 文件输入输出写错
【T1 小苹果】
【题目描述】
小Y的桌子上放着n个苹果从左到右排成一列,编号为从1到n。
小苞是小Y的好朋友,每天她都会从中拿走一些苹果。
每天在拿的时候,小苞都是从左侧第1个苹果开始、每隔2个苹果拿走1个苹果。随后小苞会将剩下的苹果按原先的顺序重新排成一列。
小苞想知道,多少天能拿完所有的苹果,而编号为n的苹果是在第几天被拿走的?
【输入】
输入的第一行包含一个正整数n,表示苹果的总数。
【输出】
输出一行包含两个正整数,两个整数之间由一个空格隔开,分别表示小苞拿走所有苹果所需的天数以及拿走编号为n的苹果是在第几天。
【输入样例】
8
【输出样例】
5 5
【参考代码1】

#include <bits/stdc++.h>
#include <cmath>
using namespace std;
int n, take = 0, cnt = 1, ans2 = 0;
int main()
{
cin >> n;
while (n>0) {
if (!ans2 && n%3==1) {
ans2 = cnt;
}
take = ceil(1.0*n/3);
// cout << "n take " << n << " " << take << endl;
n = n - take;
cnt++;
}
cout << cnt-1 << " " << ans2 << endl;
return 0;
}
【参考代码2】
解法1:模拟过程,大概有50分,可以优化到80+分
解法2:正解,模拟一下样例,找数学规律
问题1:所求的是天数,每3个看作一个周期,每次拿走的是 \(n/3\) ;
问题2,找规律发现每次一定是当元素位序 x%3==1 是才被拿走,而最开始的最后一个元素在每次拿走元素后要么被拿走,要么是新序列的最后一个,所以其位序不会对结构产生影响,只需要记录元素个数即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
void brute_force() {
int n; cin >> n;
int a = 0, b = 0, t = n;
vector<int> st(n + 1);
for (int i = 1; i <= n; i++) st[i] = i;
int cnt = 0;
while (cnt < n) {
int i = 1, p = 1;
while (i <= n) {
if (st[i] == 0) i++;
else if (st[i] && p % 3 != 1) i++, p++;
else if (st[i] && p % 3 == 1) {
if (i == n) b = a + 1;
st[i++] = 0, p++, cnt++;
}
}
a++;
}
cout << a << " " << b << endl;
}
void solve() {
int n; cin >> n;
int a = 0, b = 0;
while (n > 2) {
a++;
if (!b && n % 3 == 1) b = a;
n -= ceil(n / 3.0);
}
a += n;
if (b == 0) b = a;
cout << a << " " << b;
}
int main() {
freopen("apple.in", "r", stdin);
freopen("apple.out", "w", stdout);
solve();
fclose(stdin), fclose(stdout);
return 0;
}
【T2 公路】
【题目描述】
小苞准备开着车沿着公路自驾。
公路上一共有 n 个站点,编号为从 1 到 n 。其中站点 i 与站点 i+1 的距离为 \(v_i\) 公里。
公路上每个站点都可以加油,编号为 i 的站点一升油的价格为 \(a_i\) 元,且每个站点只出售整数升的油。
小苞想从站点 1 开车到站点 n ,一开始小苞在站点 1 且车的油箱是空的。已知车的油箱足够大,可以装下任意多的油,且每升油可以让车前进 d 公里。问小苞从站点 1 开到站点 n ,至少要花多少钱加油?
【输入格式】
输入的第一行包含两个正整数n和d,分别表示公路上站点的数量和车每升油可以前进的距离。
输入的第二行包含n-1个正整数v1, v2…vn-1,分别表示站点间的距离。
输入的第二行包含n个正整数a1, a2…an,分别表示在不同站点加油的价格。
【输出格式】
输出一行,仅包含一个正整数,表示从站点1开到站点n,小苞至少要花多少钱加油。
【输入样例】
5 4
10 10 10 10
9 8 9 6 5
【输出样例】
79
【参考代码1】

#include <bits/stdc++.h>
using namespace std;
int n, d, k=0, minn=1e9;
long long cost = 0;
int a[100005] = {0};
int v[100005] = {0};
int main()
{
cin >> n >> d;
for (int i=1; i<n; i++) {
cin >> v[i];
}
for (int i=1; i<=n; i++) {
cin >> a[i];
}
for (int i=1; i<n; i++) {
minn = min(minn, a[i]);
if (k>=v[i]) {
k = k - v[i];
continue;
}
cost += 1ll * ceil(1.0 *(v[i]-k)/d) * minn;
k = 1ll * ceil(1.0 *(v[i]-k)/d)*d - (v[i]-k);
// cout << "cost k " << cost << " " << k << endl;
}
cout << cost << endl;
return 0;
}
【参考代码2】
贪心:每次购买当前价格最低的油。
具体步骤:
0. 对于每个站点,维护一个 \([1,i]\) 的最小油价站点 \(id\) ,res[i] 记录第 i 个站点的购买量.
1. 对于当前位置 i 到达下一个站点的距离 \(v[i]\) ,需要的油量 \(t=[v[i]/id]\)
2. 可以跑的距离 为 \(t \ast d\) ,可能会跑到 \(i+1\) 站点后面,所以对 \(v[i+1]={t\ast{d}-v[i]\}\) ,也可能跑到 \(i+2\) 站点后面,所以同时对
\(i+1\) 、 \(i+2\) 维护一个合理的大小(≥0)。
3. 答案汇总:
\(ans=\sum\limits_{i=1}^{n-1} res[i] \ast a[i]\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int n, d;
int v[N], a[N], res[N];
void solve() {
scanf("%d%d", &n, &d);
for (int i = 1; i < n; i++) scanf("%d", &v[i]);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
int id = 0; // low_price_id
for (int i = 1; i < n; i++) {
if (i == 1 || a[id] > a[i]) id = i;
int t = ceil(1.0 * v[i] / d); // 需要油量
res[id] += t;
v[i + 1] -= d * t - v[i];
if (v[i + 1] < 0) {
int c = v[i + 1];
v[i + 1] = 0;
v[i + 2] += c;
}
}
LL ans = 0;
for (int i = 1; i < n; i++) ans += (LL)res[i] * a[i];
cout << ans;
}
int main() {
freopen("road.in", "r", stdin);
freopen("road.out", "w", stdout);
solve();
fclose(stdin), fclose(stdout);
return 0;
}
【T3 一元二次方程】
【题目描述】
众所周知,对一元二次方程 ax² + bx + c = 0,(a≠0),可以用下述方式求实数解:
- 计算△=b²-4ac,则:
1. 若△<0,则该一元二次方程无实数解;
2.否则△≥0,此时该一元二次方程有两个实数解x1,2=(-b±√△)/2a;
– 其中,√△表示△的算术平方根,即使得s²=△的唯一非负实数s。
-特别的,当△=0时,这两个实数解相等;当△>0时,这两个实数解互异。
例如:
- x²+x+1=0无实数解,因为△=1²-4×1×1=-3<0;
- x²-2x+1=0有两相等实数解x1,2=1;
- x²-3x+2=0有两互异实数解x1=1,x2=2;
在题面描述中a和b的最大公因数使用gcd(a,b) 表示。例如12和18的最大公因数是6, 即gcd(12,18) = 6。
现在给定一个一元二次方程的系数a,b,c,其中a,b,c均为整数且a≠0。你需要判断一元二次方程ax²+bx+c=0是否有实数解,并按要求的格式输出。
在本题中输出有理数v时须遵循以下规则:
- 由有理数的定义, 存在唯一的两个整数p和q, 满足q>0, gcd(p,q) =1且v=p/q。
- 若q=1,则输出{p};否则输出{p}/{q};其中{n}代表整数n的值;
- 例如:
- 当v=-0.5时,p和q的值分别为-1和2,则应输出-1/2;
- 当v=0时,p和q的值分别为0和1,则应输出0。
对于方程的求解,分两种情况讨论:
1.若△=b²-4ac<0,则表明方程无实数解,此时你应当输出NO;
2.否则△≥0,此时方程有两解(可能相等),记其中较大者为x,则:
(1).若x为有理数,则按有理数的格式输出。
(2).否则根据上文公式,x可以被唯一表示为x=q1+q2√r的形式,其中:
·q1,q2为有理数,且q2>0;
·r为正整数且r>1,且不存在正整数d>1使d²|r(即r不应是d²的倍数);
此时:
1.若q1≠0,则按照有理数的格式输出q1,并再输出一个加号+;
2.否则跳过这一步输出;
随后:
1.若q2=1, 则输出sqrt({r} ) ;
2.否则若q2为整数, 则输出{q2} * sqrt({r} ) ;
3.否则若q3=1/q2为整数, 则输出sqrt({r}) /{q3} ;
4.否则可以证明存在唯一整数c,d满足c,d>1, gcd(c,d) = 1且q2=c/d, 此时输出{c} * sqrt({r}) /{d} ;
上述表示中{n}代表整数n的值,详见样例。
如果方程有实数解,则按要求的格式输出两个实数解中的较大者。否则若方程没有实数解,则输出NO。
【输入】
输入的第一行包含两个正整数T,M,分别表示方程数和系数绝对值的上界;
接下来T行,每行包含三个整数a,b,c。
【输出】
输出T行,每行包含一个字符串,表示对应询问的答案,格式如题面所述。
每行输出的字符串中间不应包含任何空格。
【输入样例】
9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1
【输出样例】
1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2
【参考代码1】

#include <bits/stdc++.h>
using namespace std;
int t, m, a, b, c, delta, aa, bb, gcd1, gcd2, q2, r, ans;
int gcd(int a, int b)
{
while (b!=0) {
int r = a % b;
a = b;
b = r;
}
return a;
}
int main()
{
cin >> t >> m;
for (int i=1; i<=t; i++) {
cin >> a >> b >> c;
delta = b*b - 4*a*c;
aa = 2*a;
bb = -1*b;
if (a<0) { //当a<0时,对aa和bb进行处理,让a<0和a>0,都是统一解
aa = -1 * aa;
bb = -1 * bb;
}
q2 = 1, r = delta;
for (int i=2; i*i<=r; i++) { //对于任意的数,求出其q2和r。如果可开平方,则r=1
while (r%(i*i)==0) {
q2 = q2*i;
r = r/(i*i);
}
}
if (r==1) { //针对r==1进行特判,修改delta和bb的值
delta = 0;
bb = bb+q2;
}
gcd1 = gcd(abs(bb), aa);
gcd2 = gcd(q2, aa);
if (delta<0) {
cout << "NO" << endl;
continue;
}
if (delta==0) {
if (bb%aa==0) cout << bb/aa;
else cout << bb/gcd1 << "/" << aa/gcd1;
}
else { //即delta>0的场景
if (bb!=0) { //前半部分的输出,如果bb==0,则没有输出
if (bb%aa==0) cout << bb/aa;
else cout << bb/gcd1 << "/" << aa/gcd1;
cout << "+";
}
if (q2/gcd2!=1) cout << q2/gcd2 << "*";
cout << "sqrt(" << r << ")";
if (aa/gcd2!=1) cout << "/" << aa/gcd2; //处理分母的技巧,==1就不输出
}
cout << endl;
}
return 0;
}
【参考代码2】
分析 一道不简单的模拟题目,就是注意细节,由于是多组数据,不好骗分。
其实这个题目的描述仅仅是对问题进行了细化,主要注意一句话:分母不为负数。
对于后续的操作,我们发现输入的 a 出现的位置多为分母,所以进行转换,如果方程系数中 a 为负数,则
a, b, c 同时乘上 -1 。
其余没有什么坑点,就是多种情况的罗列了,具体看代码。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10, INF = 0x3f3f3f3f;
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
void solve() {
int t, m, a, b, c;
cin >> t >> m;
while (t--) {
cin >> a >> b >> c;
if(a < 0) a*=-1, b*=-1, c*=-1;
int delta = b * b - 4 * a * c;
if (delta < 0) cout << "NO" << endl;
else {
int n = delta;// 对 delta 质因数分解
map<int, int> mp;
for (int i = 2; i <= n; i++) {
int p = 0;
while (n && n % i == 0) n /= i, p++;
if (p) mp[i] = p;
}
if (n) mp[n] = 1;
int q1 = -b, q2 = delta > 0, r = delta > 0;
for (auto u : mp) {
int x = u.first, y = u.second;
if (y & 1) r *= x;
q2 *= pow(x, y / 2);
}
// cout<<"test: "<<q1<<" "<<q2<<" "<<r<<" "<<delta<<endl;
int d1 = gcd(q1, 2 * a), d2 = gcd(q2, 2 * a);
if (r <= 1) {
int p = q1 + q2, q = 2 * a, d = gcd(p, q);
p /= d, q /= d;
if (q < 0) p *= -1, q *= -1;
if (p == 0) { cout<<0<<endl; continue; }
cout << p;
if(q!=1) cout<<"/" << q;
cout<< endl;
} else {
int p = q1, q = 2 * a;
p /= d1, q /= d1;
if (q < 0) p *= -1, q *= -1;
if (p != 0) {
cout << p;
if (q != 1) cout << "/" << q;
}
int f = p;
p = q2, q = 2 * a, p /= d2, q /= d2;
if (q < 0) p *= -1, q *= -1;
if (f != 0 && p > 0) cout << "+";
else if (p == -1) cout << "-";
if(abs(p) != 1) cout << p;
if (p > 1) cout << "*";
cout << "sqrt(" << r << ")";
if (q != 1) cout << "/" << q;
cout << endl;
}
}
}
}
int main() {
freopen("uqe.in", "r", stdin);
freopen("uqe.out", "w", stdout);
solve();
fclose(stdin), fclose(stdout);
return 0;
}
T4 旅游巴士
【题目描述】
小Z打算在国庆假期期间搭乘旅游巴士去一处他向往已久的景点旅游。
旅游景点的地图共有n处地点,在这些地点之间连有m条道路。其中1号地点为景区入口,n号地点为景区出口。我们把一天当中景区开门营业的时间记为0时刻,则从0时刻起,每间隔k单位时间便有一辆旅游巴士到达景区入口,同时有一辆旅游巴士从景区出口驶离景区。
所有道路均只能单向通行。对于每条道路,游客步行通过的用时均为恰好1单位时间。
小Z希望乘坐旅游巴士到达景区入口,并沿着自己选择的任意路径走到景区出口,再乘坐旅游巴士离开,这意味着他到达和离开景区的时间都必须是k的非负整数倍。由于节假日客流众多,小Z在坐旅游巴士离开景区前只想一直沿着景区道路移动,而不想在任何地点(包括景区入口和出口)或者道路上逗留。
出发前,小Z忽然得知:景区采取了限制客流的方法,对于每条道路均设置了一个“开放时间”ai,游客只有不早于ai时刻才能通过这条道路。
请你帮助小Z设计一个旅游方案,使得他乘坐旅游巴士离开景区的时间尽量地早。
【输入】
输入的第一行包含3个正整数n,m,k,表示旅游景点的地点数、道路数,以及旅游巴士的发车间隔。
输入的接下来m行,每行包含3个非负整数ui,vi,ai,表示第i条道路从地点ui出发,到达地点vi,道路的“开放时间”为ai。
【输出】
输出一行,仅包含一个整数,表示小Z最早乘坐旅游巴士离开景区的时刻。如果不存在符合要求的旅游方案,输出-1。
【输入样例】
5 5 3
1 2 0
2 5 1
1 3 0
3 4 3
4 5 1
【输出样例】
6
【参考代码1】

#include <bits/stdc++.h>
using namespace std;
int n, m, k;
vector<pair<int, int>> g[10005];
int dis[10005][105];
bool bfs(int mid)
{
memset(dis, -1, sizeof(dis));
queue<pair<int, int>> q;
dis[n][0] = mid*k;
q.push({n, 0});
while (!q.empty()) {
pair<int, int> u = q.front();
int x = u.first;
int b = u.second;
q.pop();
if (dis[x][b]==0) continue;
for (int i=0; i<g[x].size(); i++) {
pair<int, int> pr = g[x][i];
if (dis[x][b]-1 < pr.second) continue;
int y = pr.first, p = (b+k-1)%k;
if (dis[y][p]!=-1) continue;
dis[y][p] = dis[x][b] - 1;
q.push({y, p});
}
}
if (dis[1][0] == -1) return false;
else return true;
}
int main()
{
cin >> n >> m >> k;
for (int i=1; i<=m; i++) {
int u, v, a;
cin >> u >> v >> a;
g[v].push_back({u, a});
}
int l = 0, r = 2000000 / k, ans=-1;
while (l<r) {
int mid = (l+r)/2;
if (bfs(mid)) {
ans = mid * k;
r = mid;
}
else l = mid+1;
}
cout << ans << endl;
return 0;
}
【参考代码2】
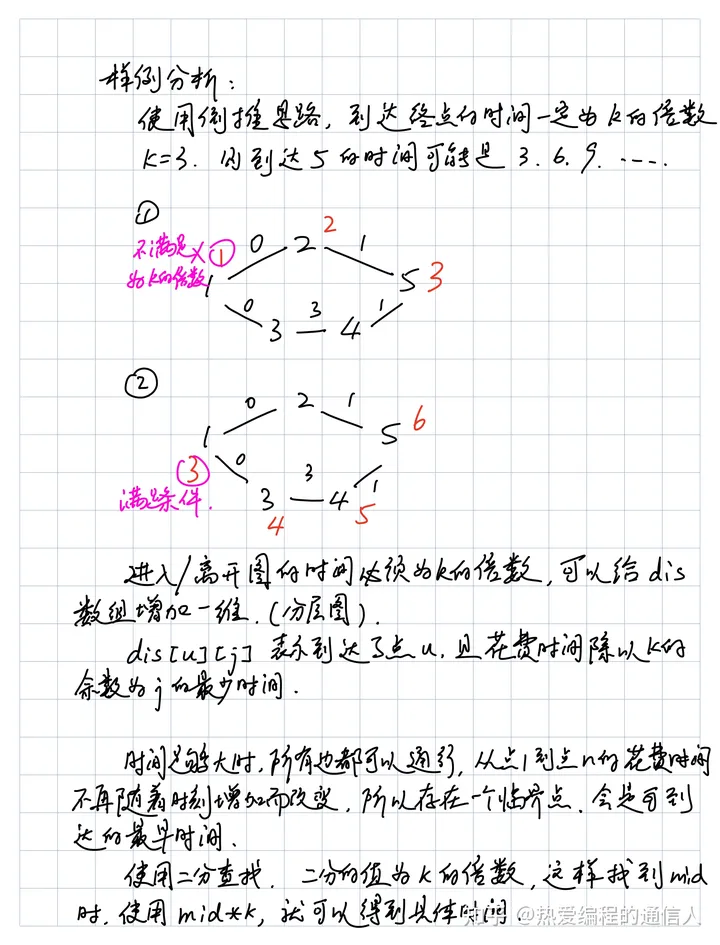
最短路的基础上多了条件:
1. 起点和终点时间为 k 的倍数.
2. 通过 i 点的时间不能 \(