【题目】
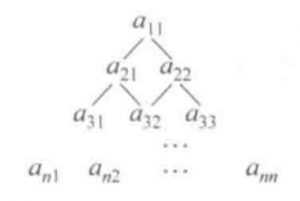
有正实数构成的数字三角形排列形式如图所示。第一行的数为 \(a(1,1)\) ,第二行 \(a(2,1)\),\(a(2,2)\),第n行的数为 \(a(n,1)\),\(a(n,2)\),…,\(a(n,n)\)。从 \(a(1,1)\) 开始,每一行的数 \(a(i,j)\) 只有两条边可以分别通向下一行的两个数 \(a(i+1,j)\) 和 \(a(i+1,j+1)\) 。
用动态规划算法找出一条从\(a(1,1)\) 向下通道 \(a(n,1)\),\(a(n,2)\),…,\(a(n,n)\) 中某个数的路径,使得该路径上的数之和最大。
令 \(C[i][j]\) 是从 \(a(1,1)\) 到 \(a(i,j)\) 的路径上的数的最大和,并且 \(C[i][0]=C[0][j]=0\),则 \(C[i][j]=(?)\)
A. \(max{C[i-1][j-1],C[i-1][j]}+a(i,j)\)
B. \(C[i-1][j-1]+C[i-1][j]\)
C. \(max{C[i-1][j-1],c[i-1][j]}+1\)
D. \(max{C[i][j-1],C[i-1][j]}+ a(i,j)\)
【考点】
数塔问题。
动态规划算法(DP,Dynamic Programming)是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
【解析】
经典的数塔问题。
路径只能从左上方和上方过来。
从上一层对应的两个状态中较大的转移过来即可。
每个点只能从上方两个点过来,自然取最大的加a(i,j)。
答案选择:A
参考:https://www.cnblogs.com/HIIM/p/12722862.html
参考:https://blog.csdn.net/qq_42795064/article/details/106867097